Bac 2024 : sujets corrigés de l'épreuve de Spécialité PC 🎓
Nos profs décryptent l'épreuve pour toi !
Tu cherches les sujets corrigés de l'épreuve de spécialité PC pour savoir si tu as réussi ton épreuve ? Cet article est pour toi ! Nos professeurs ont fait l’examen en même temps que toi ! Retrouve tous tes corrigés express du Bac 2024 à l’issue de chaque examen pour savoir si tu as géré pendant l'épreuve.
Voici des éléments de réponses possibles pour les exercices proposés.
Exercice 1 : Vers le bleu de thymol
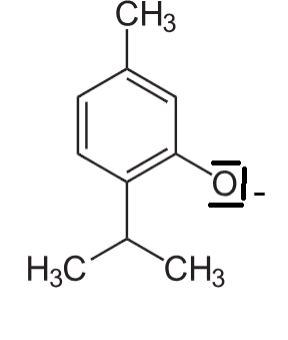
Q1- La formule semi-développée du Thymol est :

Il s’agit du groupe caractéristique OH, la famille des alcools.
Q2- La formule de Lewis de l’ion thymolate est :
Q3- Le chromatogramme obtenu présente plusieurs tâches, on a donc un mélange de Thymol.
Q4- $\rm R-{O^{-}}_{aq}+H_3 O^{+}{ }_{a q}=R-O H_{(a q)}+H_2 0_{(l)}$
Q5- À l’issue de la décantation, le thymol se trouve à la phase liquide et a une densité plus faible que l’eau, elle sera au-dessus de l’eau.
Q6- On sait que l’on peut au maximum 2 g de Thymol avec 100 g de Thym. Seulement, lors de l’extraction du Thymol, on a un rendement de : $\dfrac{31}{100} \times \dfrac{53}{100}=16,48~ \%$
#NEWPAGE#
On a donc pour 1 g de thymol, il faut avoir : $\dfrac{1}{0.1648 \times \frac{2}{100}}=304~g$ de thym.
Q7- P2 est un isomère (même nombre d’éléments chimiques que le thymol) mais P4 ne l’est pas (plus d’éléments chimiques).
Q8- Un catalyseur est une espèce chimique permettant une réaction chimique ou augmentant la vitesse d’une réaction. Elle permet donc de réduire la température de la synthèse puisque la température est un accélérateur de réaction.
Q9- L’ajout de propène en excès dans cette synthèse industrielle permet de jouer ce rôle de catalyseur avec une température d’ébullition de -47,7°C.
Q10- Le m-crésol et le thymol peuvent a priori être séparés car ils ont des masses molaires différentes. Le m-crésol étant plus léger que le thymol, on récupère en premier le m-crésol.
Q11- On a : $n_{\text {thymol}}=\dfrac{m}{\mathrm M}=\dfrac{1}{150.2}=6.7 \times 10^{-3} \mathrm{~mol} = n_{\text {mcresol_reagi}}$
On en déduit que : $m=\mathrm M_{\text {mcresol}} \times n_{\text {mcresol_reagi}}=0,72~ \mathrm{~g}$
Et le volume de m-cresol qui est de : $\mathrm V=\dfrac{m}{\rho}=\dfrac{0,72}{1,03}=0,69~ \mathrm{ml} <1~ \mathrm{ml}$
Q12- $\rm BTH^-$ est une espèce amphotère car selon son couple, elle peut être base ou acide comme l’eau par exemple.
Q13- La formule de la constante d’acidité est donnée par :
$\rm K_A=\dfrac{\left[A^{-}\right] \times\left[H^{+}\right]}{[A H]}$
Q14- À l’équivalence, sur la figure 5, les courbes de $\rm BTH^-$ et $\rm BT^{2-}$ se croisent et on a $\rm pH=pK_A=8.8$.
On peut remplacer la phénolphtaléine par le bleu de thymol car celui-ci a une zone de virage correspondant au $\rm pK_A$ obtenu.
Sur la figure 6, on voit des longueurs d’onde autour de 500 nm ce qui signifie un changement de couleur du jaune au bleu.
Q15- Les valeurs sont très proches avec un écart de à 0.1 sur le $\rm pK_A$.
Exercice 2 : Observation d’un avion en vol
1. Une lunette afocale est une lunette dont le foyer image de l’objectif $\rm F'_1$ est confondu avec le foyer objet de l’oculaire $\rm F_2$.
2. Les réponses sont sur le schéma ci-dessous.
3. La construction est sur le schéma ci-dessous.
Les angles $\alpha$, $\alpha'$ sont notées $\theta$, $\theta'$.

4. On a : $\alpha=\dfrac{L}{h}=\dfrac{44.5}{10~400}=4,3 \times 10^{-3} \mathrm{rad} > 3 \times 10^{-4} \mathrm{rad}$ donc objet discernable. On pourra distinguer l'avion de l'avant de sa queue à l'œil nu.
5. Voir schéma. $\rm G= \dfrac{\alpha'}{\alpha}$
6. Avec la lunette astronomique, pour le grossissement minimal de 16 , on a :
$\alpha'=16 \times \dfrac{l}{h}=\dfrac{16 \times 0,23}{10~400}=3,5 \times 10^{-4} \mathrm{rad} > 3 \times 10^{-4}~ \mathrm{rad}$
On pourra distinguer le hublot.
7. Il s'agit de l'effet Doppler.
8. On a : $f_{\mathrm A} = 2,2~ \mathrm{kHz}$ et $f_{\mathrm E}=1,5~ \mathrm{kHz}$.
Il s'agit de la proposition $\mathrm{B}$ car la $\mathrm{A}$ n'est pas homogène à une fréquence, les propositions $\mathrm{C}$ et $\mathrm{D}$ ne sont pas cohérentes (pas d'aller-retour pour $\mathrm{D}$ et $\mathrm{C}$ incohérente avec les valeurs des fréquences obtenues éloignées, supérieur à la fréquence proche).
9. On a : $\dfrac{f_{\mathrm A}}{f_{\mathrm E}} = \dfrac{c+v}{c-v}=\dfrac{22}{15}$.
Soit : $c \times\left(-1+\dfrac{22}{15}\right)=v \times\left(1+\dfrac{22}{15}\right)$
$v=\dfrac{c \times\left(-1+\frac{22}{15}\right)}{\left(1+\frac{22}{15}\right)}=64,3 \mathrm{~m} / \mathrm{s}=231,5~ \mathrm{~km} / \mathrm{h}$.
Avec $c=340 \mathrm{~m} / \mathrm{s}$.
La vitesse obtenue est cohérente avec une vitesse d'atterrissage moyenne d'un avion qui est de $260 \mathrm{~km} / \mathrm{h}$.
Exercice 3 : Accéléromètre d’un mobile multifonction
Q1. Le smartphone est soumis à l'accélération de pesanteur.
D'après la 2nde loi de Newton, on a : $m \times a_z=-m \times g$
Soit : $a_z=-g$.
Q2. On a : $\boldsymbol{a}_{\mathrm{z}}=\dfrac{d v_{\mathrm{z}}}{d t}=-g$
On en déduit : $v_z(t)=-g \times t+v_0=\frac{d z}{d t}$
En faisant la primitive, on a : $z(t)=-g \times \dfrac{t^2}{2}+v_0 \times t+z_0$.
Les conditions initiales étant que l'on est sans vitesse initiale et à une altitude égale à $\mathrm{H}$, on en déduit que : $z(t)=-g \times \frac{t^2}{2}+\rm H$ avec $v_0=0$ et $z_0=\rm H$.
Q3. L'énergie mécanique se conserve car le système n'est pas soumis au frottement.
L'énergie mécanique est constante et égale à : $\rm E_m=E_c+E_p$
$\rm E_c$ est l'énergie cinétique et $\rm E_p$, l'énergie potentielle.
$\mathrm{A} \mathrm{t}=0$, la vitesse initiale est nulle et le smartphone à une altitude $\mathrm{H}$.
On en déduit que : $\mathrm{E_m} = m \times g \times h$. (L'énergie cinétique est nulle, l'énergie mécanique vaut l'énergie potentielle).
Q4. L'évolution temporelle de la composante $a_z$ n'est pas compatible avec le modèle de chute libre car elle n'est plus constante au cours du temps.
Q5. La courbe A correspond à l'énergie potentielle de pesanteur (en descendant, on diminue en altitude). La courbe $\mathrm{B}$ correspond à l'énergie cinétique (nulle au début). On rappelle que l'énergie mécanique est la somme de ces deux énergies.
Q6. On a à $\mathrm{t}=0,45 \mathrm{~s}$, $\mathrm{E_C}=\dfrac{1}{2} \times m \times v^2=2,3 \mathrm{~J}$ avec $m=182 \mathrm{~g}$
Soit : $v=\sqrt{\dfrac{2 \times \rm E_C}{m}}=\sqrt{\dfrac{2 \times 2,3}{0,182}}=5 \mathrm{~m} / \mathrm{s}$
Q7. Le smartphone est soumis à une force de frottement et son poids.
On a la seconde loi de Newton suivante : $m \times a_z=-m \times g+f$
Soit $f=m \times a_z+m \times g=m \times\left(a_z+g\right)$
Q8. Sur la figure 4, cela correspond à l'ordonnée à l'origine pour $v=0$, on a : $g=9,8 \mathrm{~m} \cdot \mathrm{s}^{-2}$
Q9. On a : $a_z=0,0555 \times v^2-9,80$
$f=m \times a_z+m \times g=m \times\left(a_z+g\right)=m \times\left(0,0555 \times v^2-9,80+9,8\right) =m \times 0,0555 \times v^2$
On pose : $k=m \times 0,0555=0,01 \mathrm{~kg} / \mathrm{m}$. On a : $f=k \times v^2$
Q10. En fin de chute, on a : $v^2=25(\mathrm{~m} / \mathrm{s})^2$
On a : $f=0,01 \times 25=0,25 ~\rm N$ et $\rm P=0,182 \times 9,80=1,79 ~N$
Cela représente $14 ~\%$ du poids du smartphone, le frottement n'est pas négligeable.



