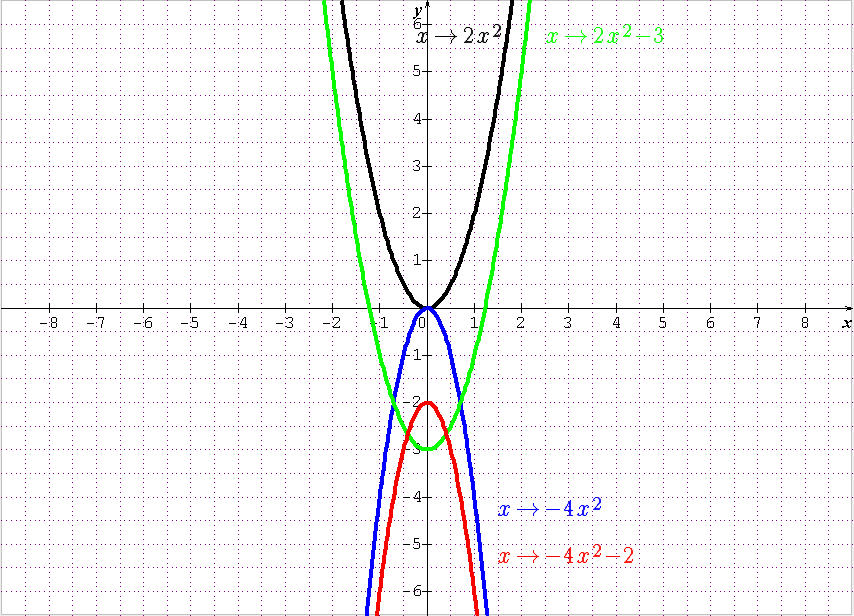
Fonctions $x\mapsto ax^2$, $a\neq 0$ un réel
- Si $a > 0$, la courbe représentative de cette fonction est une parabole orientée vers le haut.
Elle est située au-dessus de l’axe des abscisses. - Si $a < 0$, la courbe représentative de cette fonction est une parabole orientée vers le bas.
Elle est située au-dessous de l’axe des abscisses.
Dans tous les cas, la courbe représentative de cette fonction admet pour extremum le point O(0 ; 0) et pour axe des symétrie la droite d’équation $x = 0$.
Fonctions $x\mapsto ax^2 + b$, $a\neq 0$ et $b$ deux réels
- Si $a > 0$, la courbe représentative de cette fonction est une parabole orientée vers le haut.
- Si $a < 0$, la courbe représentative de cette fonction est une parabole orientée vers le bas.
Dans tous les cas, la courbe représentative de cette fonction admet pour extremum le point S(0 ; $b$) et pour axe des symétrie la droite d’équation $x = 0$.
Exemples de représentations graphiques