Construction d’une image à travers une lentille mince convergente
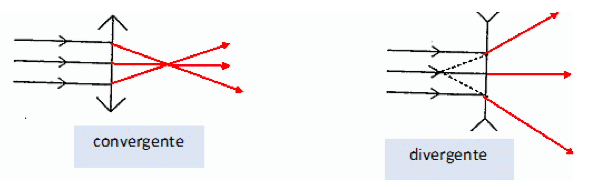
Une telle lentille peut donner d’un objet réel $\rm AB$ :
- Une image sur un écran, appelée image réelle, lorsque $\rm AB$ est situé avant le foyer principal objet $\rm F$ de la lentille ;
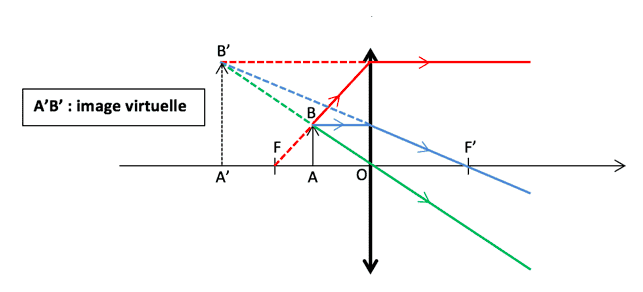
- Une image non visible sur un écran, appelée image virtuelle, lorsque $\rm AB$ est situé entre le foyer principal objet $\rm F$ et le centre optique $\rm O$ de la lentille. C’est ce qui est observé à travers une loupe.
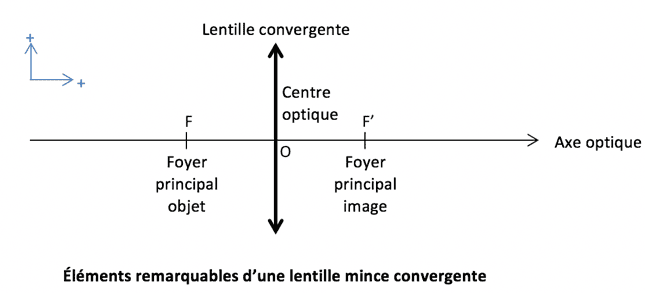
Quelques principes sont à respecter pour la construction d’une image à travers une lentille. On considère que des rayons lumineux, symbolisés par des traits fléchés, en provenance d’un objet $\rm AB$, atteignent la lentille. Seuls trois de ces rayons sont remarquables et permettent la construction de l’image $\rm A’B’$ de l’objet $\rm AB$ à travers cette lentille :
- En bleu, un rayon issu de $\rm AB$, parallèle à l’axe optique, ressort de la lentille en passant par son foyer principal image $\rm F’$ ;
- En vert, un rayon issu de $\rm AB$ traverse la lentille en passant par son centre optique, sans subir de déviation ;
- En rouge, un rayon issu de $\rm AB$ passant par le foyer principal objet $\rm F$ de la lentille, ressort de la lentille parallèle à son axe optique.

Relations applicables aux lentilles
1) Relation de conjugaison
Cette relation met en lien la position de l’objet et celle de l’image :
$\rm f = \dfrac{1}{OA'} = \dfrac{1}{OA} + \dfrac{1}{OF'}$
2) Relation de grandissement
Le grandissement $\gamma$ correspond au rapport entre la taille de l’image rendue par la lentille et celle de l’objet. Le grandissement est aussi égal au rapport entre la distance de l’image au centre optique et celle de l’objet au centre optique :
$\rm \gamma = \dfrac{A'B'}{AB}$
Si $\gamma < 0$, le sens de l’image est inversé par rapport à celui de l’objet.