Travail d’une force constante
Le travail d'une force $ \rm \vec {F}$ constante dont le point d'application effectue un déplacement rectiligne $\rm AB = l$, faisant un angle $\alpha$ avec la direction de la force, est donné par la relation :
$\rm W = F \times l \times \cos(\alpha)$
Avec $\rm W$ le travail en joule (J), $\rm F$ la force en newton (N) et $\rm l$ la longueur de déplacement en mètres (m).
On distingue plusieurs cas
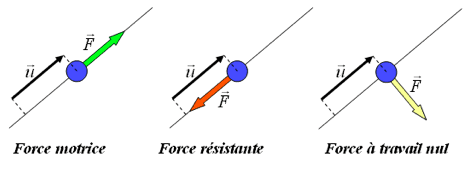
- Une force est motrice si son sens favorise le déplacement (le travail est positif)
- Une force est résistante si elle s’oppose au déplacement (le travail est négatif)
- Le travail est nul si le point d’application de la force ne se déplace pas, ou si la direction de la force est perpendiculaire au déplacement.
Différentes formes d’énergie et conversion dans les machines
L’énergie $\rm E$ se mesure en Joules. Nous la retrouvons sous plusieurs formes :
- Énergie rayonnante (Lumineuse)
- Énergie chimique (provenant des combustions ou tout autre réaction chimique)
- Énergie électrique
- Énergie nucléaire
- Énergie mécanique (provenant du mouvement d’un objet et de sa position en hauteur)
- Énergie thermique (sous forme de chaleur)
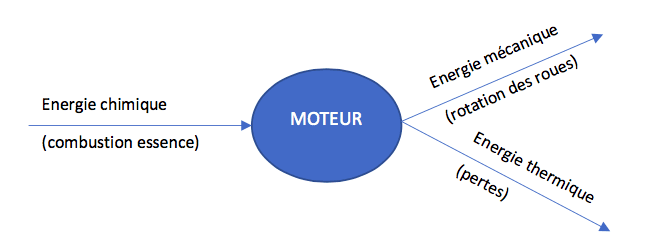
Les machines convertissent une forme d’énergie qui lui est fournie pour la restituer sous une autre forme.
Exemple d’un moteur thermique :