Pour repérer la position d’un point en mouvement dans l’espace, il est possible d’utiliser les trois systèmes de coordonnées suivants :
1. Coordonnées cartésiennes
Les coordonnées cartésiennes $(x, y, z)$ peuvent être utilisées pour étudier tout point P en mouvement quelconque dans l'espace. Toutefois, si le point décrit un cercle, une ellipse, une hélice, etc., ou subit une rotation, on préférera simplifier les calculs avec l’utilisation des coordonnées cylindriques ou sphériques décrites plus bas.
La base cartésienne orthonormée directe $(\vec{u_x}, \vec{u_y}, \vec{u_z})$ est une base fixe (la dérivée de chacun de ces trois vecteurs est nulle).
- Expression de la position
$\vec{OP} = x\vec{u_x}+y\vec{u_y}+z\vec{u_z}$
- Expression de la vitesse
$\vec{v} = \dot x\vec{u_x}+\dot y \vec{u_y}+\dot z\vec{u_z}$
- Expression de l'accélération si r est une constante
$\vec{a} = \ddot x\vec{u_x}+\ddot y \vec{u_y}+\ddot z\vec{u_z}$
2. Coordonnées cylindriques
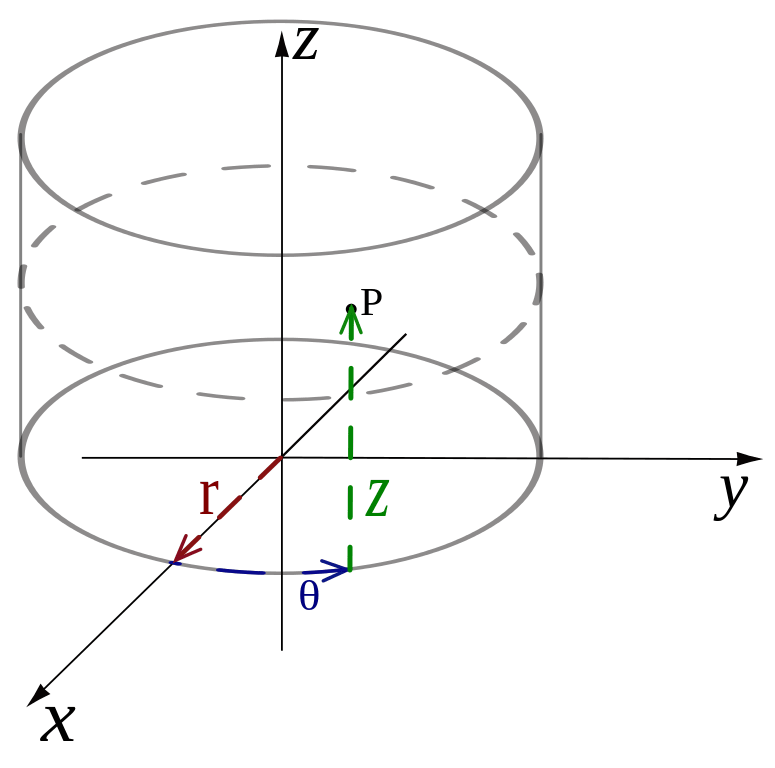
Les coordonnées cylindriques $(r, \theta, z)$ sont en particulier utilisées pour étudier tout point M en mouvement circulaire, hélicoïdal, etc.
La base cylindrique orthonormée directe liée au point M se note $(\vec{u_r}, \vec{u_\theta}, \vec{u_z})$. Si le mouvement se fait en 2D, c’est-à-dire dans un plan (z=0) alors on parle de base polaire $(\vec{u_r}, \vec{u_\theta})$.
Attention : $(\vec{u_r}, \vec{u_\theta})$ est une base mobile liée au point P, par conséquent la dérivée de ces deux vecteurs n’est pas nulle.
- Expression de la position
$\vec{OP} = r\vec{u_r}+z\vec{u_z}$
- Expression de la vitesse
$\vec{v} = \dot r\vec{u_r}+r \dot \theta \vec{u_\theta}+\dot z\vec{u_z}$
- Expression de l’accélération
$\vec{a} = (\ddot r - r\dot \theta ^2 )\vec{u_r}+(r\ddot \theta +2\dot r \dot \theta) \vec{u_\theta}+\ddot z\vec{u_z}$
3. Coordonnées sphériques
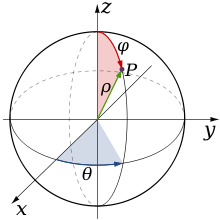
Les coordonnées sphériques $(\rho, \theta, \phi)$ sont en particulier utilisées pour étudier un mouvement de rotation.
La base sphérique orthonormée directe liée au point P se note $(\vec{u_\rho}, \vec{u_\theta}, \vec{u_\phi})$.
- Expression de la position
$\vec{OP} = \rho \vec{u_\rho}$
- Expression de la vitesse
$\vec{v} = \dot \rho \vec{u_\rho}+ \rho \dot \theta \vec{u_\theta}+\rho sin (\theta) \dot \phi \vec{u_\phi}$



