On considère une population qui possède 2 caractères qualitatifs $A$ et $B$ qui peuvent posséder plusieurs modalités : $A_j$ et $B_i$.
On obtient le tableau de contingence suivant avec $O_{ij}$ les effectifs observés :
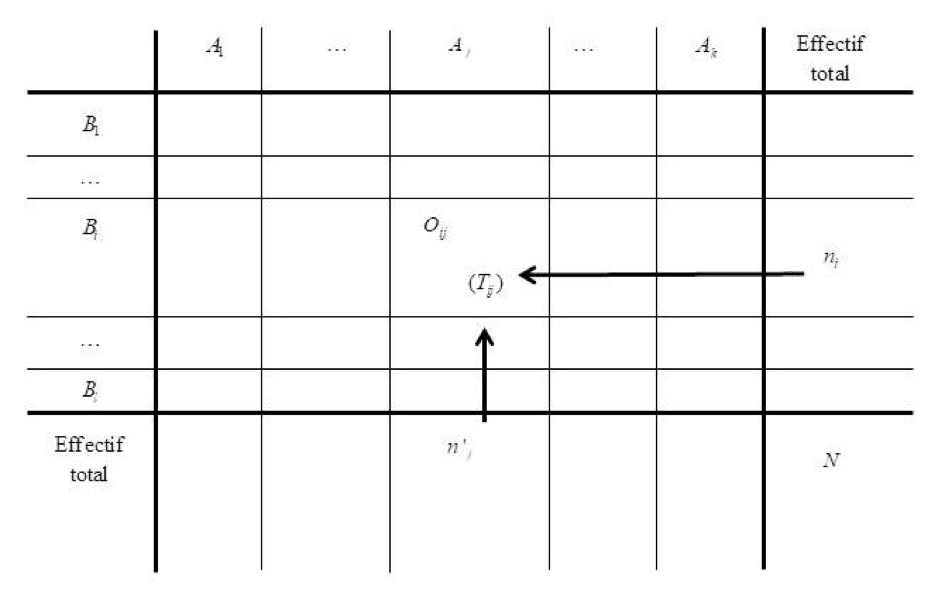
Les effectifs théoriques (indiqués ici entre parenthèses) se calculent de la façon suivante: $T_{ij}=\displaystyle\frac{n_i\times n’_j}{N}$
Remarque : un effectif théorique n’est pas toujours un nombre entier mais on n’arrondit pas le résultat afin que les calculs soient le plus précis possible.
$\nu=(k-1)(l-1)$ représente le nombre de degrés de liberté du test.
Principe du test du $\chi^2$ de Pearson (ici test d’indépendance) :
- On fixe l’hypothèse nulle : $H_0$ : « Il y a indépendance entre les caractères $A$ et $B$ ».
- On se fixe un risque $\alpha$ (par exemple 5%) a priori.
- On vérifie les conditions d’utilisation : $N\geq 30$, $n\geq 5$ où $n$ représente les effectifs de classe.
- On calcule le paramètre du test :
$\chi^2=\displaystyle\sum_{i=1}^l\sum_{j=1}^k\frac{(O_{ij}-T_{ij})^2}{T_{ij}}$ - On conclut au risque $\alpha$ en lisant $\chi^2_0$ dans la table du $\chi^2$ de Pearson (avec comme paramètres $\nu$ et $\alpha$).
- Si $\chi^2< \chi^2_0$ on ne rejette pas $H_0$
- Sinon on rejette $H_0$.
Remarque : Pour $\alpha$=5% et ddl=1, $\chi^2_0=3,84$.
En cas de rejet de $H_0$, on peut déterminer le degré de signification (p-value) : c’est la plus petite valeur de risque pour laquelle il y a rejet de $H_0$.
Remarque : Si $ 30\leq N<50$ et $n<5$ on utilise la formule avec la correction de Yates (elle n’est valable que pour les tableaux $2\times 2$) : $\chi^2=\displaystyle\sum_{i=1}^2\sum_{j=1}^2\frac{(|O_{ij}-T_{ij}|-0,5)^2}{T_{ij}}$


