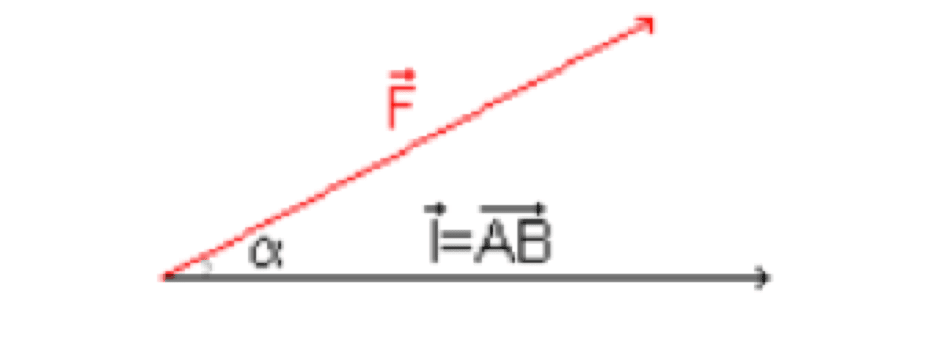
Définition : Le travail, noté $\rm W_{AB}(\vec F)$ d'une force constante $\rm \vec F$, sur un déplacement $\rm AB$ de son point d'application, est le produit scalaire de la force $\bf \vec F$ par le déplacement $\bf \overrightarrow{AB}$.
On écrit ainsi : $\begin{array}{|c|}\hline \rm W_{AB}(\vec F) = \vec F \cdot \overrightarrow{AB}\\ \hline \end{array}$ ou $\begin{array}{|c|}\hline \rm W_{AB}(\vec F) = F \cdot AB \cdot \cos \alpha \\ \hline \end{array}$
\[\scriptstyle \left\{\begin{array}{lll}
\rm W_{AB}(\vec F) : \text{Travail de la force } \vec F \text{ en Joules (J)}\\
\rm \overrightarrow{AB} : \text{Vecteur déplacement du point d'application de la force.}\\
\text{AB en mètres (m).}\\
\rm \alpha : \text{Angle existant entre les vecteurs, } \vec F \text{ et } \overrightarrow{AB},\\
\text{ en ° (degré) ou rad (radian)}\\
\end{array}\right.\]
Travail du poids :
$\rm W_{AB}(\vec P) = \vec P \cdot \overrightarrow{AB} = \mathcal{m\vec g}\cdot \overrightarrow{AB}$ $=mg \cdot \rm AB \cdot \cos (\alpha)$
Or dans le triangle $\rm AOB$ représenté ci-dessous :
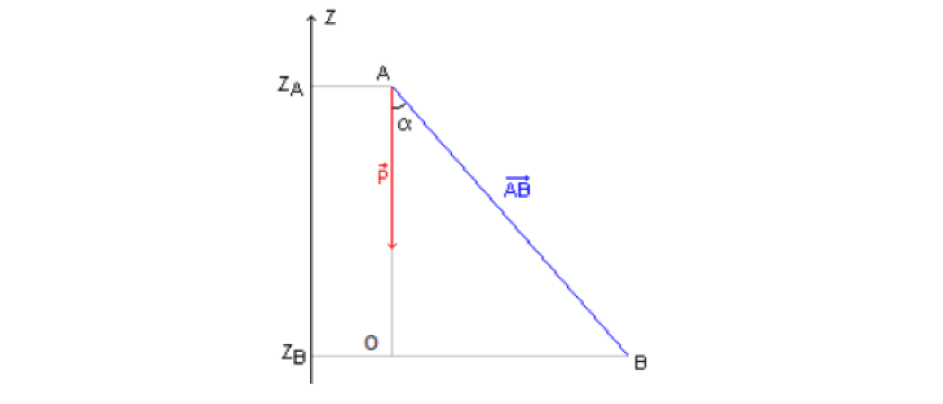
\[\scriptstyle \rm\cos(\alpha) = \frac{AO}{AB}
\begin{array}{lll}
\Rightarrow \mathrm{AB \cdot \cos(\alpha) = AO} = z_A - z_o \\
\Rightarrow \mathrm{AB} \cdot \cos(\alpha) = z_A - z_B \\
\Rightarrow \mathrm{W_{AB}(\vec P)} = mg \cdot \mathrm{AB} \cdot \cos(\alpha) = mg(z_A - z_B)\\
\end{array}\]
Bilan : Le travail du poids est défini par la relation suivante :
\[\begin{array}{|c|}
\hline
\mathrm{W_{AB}(\vec P)} = mg (z_A - z_B)\\
\hline
\end{array}\]
Il ne dépend que de la variation d'altitude $z_A - z_B$.
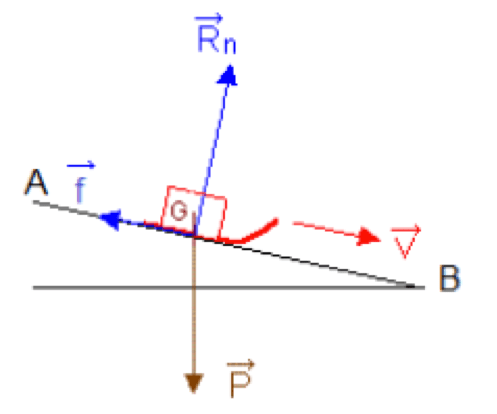
Travail d'une force de frottement :
Le travail de la force de frottements, sur le chemin $\rm AB$ s'exprime ainsi :
\[\mathrm{W_{AB}} = \vec f \cdot \mathrm{\overrightarrow{AB}} = f \cdot \mathrm{AB} \cdot \cos (180°) = -f \cdot \rm AB\]
Théorème de l'énergie cinétique :
\[\displaystyle \mathrm{Ec} = \frac{1}{2} \times \mathrm m \times v^2\]
Avec :
- La masse $\rm m$ exprimée en kilogramme $\rm (kg)$
- La vitesse $v$ exprimée en mètres par seconde $\rm(m/s)$
- L'énergie cinétique $\rm Ec$ exprimée en Joules $\rm(J)$
La variation d'énergie cinétique $\rm Ec$ d'un solide entre $\rm A$ et $\rm B$ est liée au travail des forces appliquées entre $\rm A$ et $\rm B$ = c'est le théorème de l'énergie cinétique :
\[\displaystyle \rm Ec_B - Ec_A = \sum W_{AB} (\vec F)\]
\[\displaystyle \frac{1}{2} \cdot \mathrm m \cdot v_B^2 - \frac{1}{2} \cdot \mathrm m \cdot v_A^2 = \Delta \rm Ec = \sum W_{AB}(\vec F)\]
Energie mécanique :
L'énergie mécanique, notée $\rm Em$, d'un corps est la somme de son énergie cinétique $\rm Ec$ et son énergie potentielle de pesanteur $\rm Epp$ :
\[\rm Em = Ec + Epp\]
On appelle énergie potentielle de pesanteur d'un solide $\rm S$ de masse $\rm m$ situé à l'altitude $z$ la quantité.
\[\scriptstyle \color{blue}{\begin{array}{|c|}
\hline
\color{black}{\mathrm{Epp = m} \cdot g \cdot z} \\
\hline
\end{array}}
\color{black}{\text{ et } \left\{\begin{array}{lll}
\rm _{Epp} \text{ Energie potentielle de pesanteur en Joules (J)}\\
\rm _m \text{ Masse du solide en kilogramme (kg)}\\
_z \text{ Altitude du solide en mètre (m).}\\
\end{array}\right.}\]
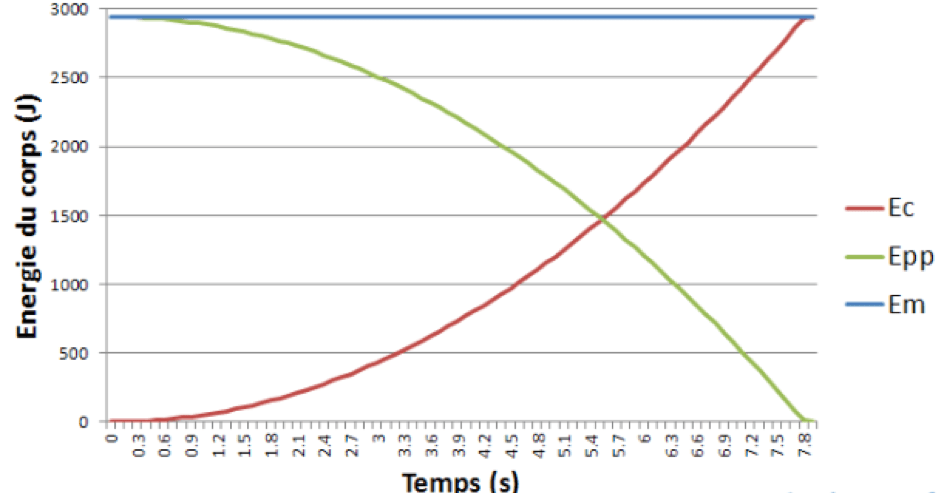
Conservation de l'énergie mécanique :
Au cours d'une chute sans frottements, l'énergie mécanique est constante : on dit qu'elle se conserve. La diminution de l'énergie potentielle de pesanteur est compensée par l'augmentation de l'énergie cinétique.