Le référentiel est un endroit de référence par rapport auquel on étudie le mouvement d’un mobile.
A chaque référentiel est associé :
- Un repère d’espace pour quantifier la position ;
- Un repère de temps (une horloge) pour associer une date à chaque position.
La position d'un mobile $\rm M$ dans un repère $(\mathrm O, \vec i, \vec j, \vec k)$ est donnée par son vecteur-position $\rm \overrightarrow{OM}$ :
\[\scriptstyle \rm \overrightarrow{OM}(\cal t)\left(\begin{array}{lll} x(t)\\ y(t) \\ z(t)\end{array}\right) \Leftrightarrow \overrightarrow{\rm OM}(t) = x(t) \vec i + y(t) \vec j + z(t) \vec k \]
L'ensemble des points occupés successivement par le mobile $\rm M$ au cours du temps est appelé trajectoire.
Le vecteur vitesse :
Le vecteur-vitesse $\vec v(t)$ caractérise la variation du vecteur-position en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.
Le vecteur-vitesse instantanée au point $\rm M$, s'écrit donc :
\[\begin{array}{|c|}
\hline
\overrightarrow{v(t)} = \displaystyle \frac{d\overrightarrow{\rm OM}}{dt}\\
\hline
\end{array}
\left\{\begin{array}{ll}
t \text{ en s}\\
\rm OM \text{ en m}\\
v \text{ en } \rm m.s^{-1}
\end{array}\right.\]
\[\scriptstyle \vec v(t) = v_x(t)\vec i + v_y(t)\vec j + v_z(t)\vec k =\dot{x}\vec i + \dot{y}\vec j + \dot{z}\vec k\]
Notation :
- $v_x(t) = \dot{x} = \displaystyle \frac{dx}{dt}$ ;
- $v_y(t) = \dot{y} = \frac{dy}{dt}$ ;
- $v_z(t) = \dot{z} = \frac{dz}{dt}$.
Les caractéristiques du vecteur-vitesse sont les suivantes :
\[\scriptstyle \overrightarrow{v(t)} \left\{\begin{array}{lll}
\text{ direction : tangent à la trajectoire}\\
\text{ sens : celui du mouvement}\\
\text{ valeur (norme)} : \left\|\vec v \right\| = v = \sqrt{v_x^2 + v_y^2 + v_z^2}
\end{array}\right.\]
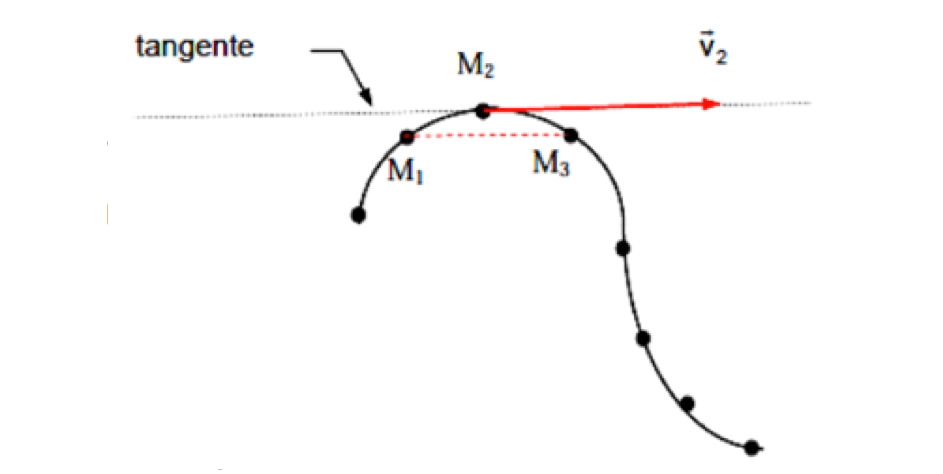
Construction d'un vecteur-vitesse :
Le vecteur-vitesse moyen $\vec v(t_2)$ au point $\rm M_2$ à la date $t_2$ s'écrit :
\[\begin{array}{|c|}\hline
\vec v (t_2) = \displaystyle \frac{\rm \overrightarrow{M_1M_3}}{t_3 - t_1}\\
\hline
\end{array}\]
Le vecteur-vitesse $\vec v (t_2)$ possède :
- Une direction : la tangente à la trajectoire au point $\rm M_2$, parallèle à la droite $\rm M_1M_3$.
- Un sens : celui du mouvement.
- Une valeur : $v_2 = \displaystyle \frac{\rm M_1M_3}{t_3-t_1} = \frac{\rm M_1M_3}{2\rho}$ $v_2$ s'exprime en $\rm m.s^{-1}$.
- Une longueur : donnée par une échelle des vitesses (exemple : $\rm 1~cm \leftrightarrow 0,1~m.s^{-1}$).
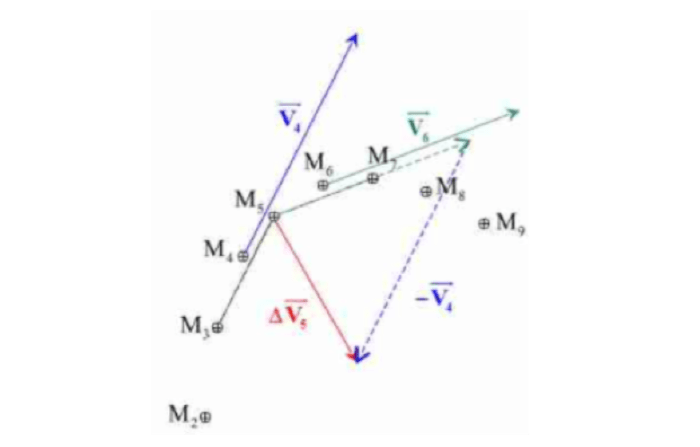
Le vecteur variation de vitesse :
Comment construire le vecteur $\bf \overrightarrow{\Delta V_5} = \overrightarrow{V_6} - \overrightarrow{V_4}$ ?
- Tracer les vecteurs vitesses $\rm \overrightarrow{V_4}$ et $\rm \overrightarrow{V_6}$.
- Au point $\rm M_5$, reconstruire le vecteur $\rm \overrightarrow{V_6}$.
- Construire le vecteur $\rm -\overrightarrow{V_4}$ depuis l'extrémité du vecteur $\rm \overrightarrow{V_6}$ reconstruit juste avant.
- Le vecteur $\rm \overrightarrow{\Delta V_5}$ est le vecteur qui joint l'origine de $\rm \overrightarrow{V_6}$, point $\rm M_5$, à l'extrémité de $\rm -\overrightarrow{V_4}$.
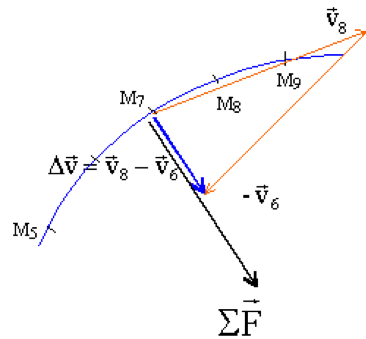
La somme des forces appliquée au système :
\[\displaystyle \sum \mathrm{\vec F_{ext} = m} \times \Delta \vec v / \Delta t\]
Le rôle de la masse du système :
Plus la masse du système est grande, plus la variation du vecteur vitesse est faible pour une même somme des forces appliquées.
Le vecteur-accélération $\vec a(t)$ caractérise la variation du vecteur-vitesse en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps du vecteur-vitesse.
Le vecteur-accélération au point $\mathrm M_i$ s'écrit donc :
\[\begin{array}{|c|}
\hline
\overrightarrow{a(t)} = \displaystyle \frac{\overrightarrow{dv}}{dt} = \frac{d^2\overrightarrow{\rm OM}}{dt^2}\\
\hline
\end{array}
\left\{\begin{array}{ll}
t \text{ en s}\\
v \text{ en } \rm m.s^{-1} \\
a \text{ en } \rm m.s^{-2}
\end{array}\right.\]
$\vec a (t) = a_x (t) \vec i + a_y(t) \vec j + a_z(t)\vec k$ $= \dot{v_x}\vec i + \dot{v_y} \vec j + \dot{v_z}\vec k$ $= \ddot{x} \vec i + \ddot{y} \vec j + \ddot{z}\vec k$
Notation : $a_x(t) = \displaystyle \frac{dv_x}{dt} = \frac{d^2x}{dt^2} = \ddot{x}$. De même pour $a_y$ et $a_z$.
Les caractéristiques du vecteur-accélération sont les suivantes :
\[\scriptstyle\overrightarrow{a(t)} \left\{\begin{array}{lll}
\text{ direction : celle du vecteur } \overrightarrow{\Delta v(t)}\\
\text{ sens : celui du vecteur } \overrightarrow{\Delta v(t)}\\
\text{ valeur (norme)} : a = \frac{\Delta v}{\Delta t} = \left\|\vec a \right\| =\sqrt{a_x^2 + a_y^2 + a_z^2}
\end{array}\right.\]