En quoi consiste l’expérience des trous d’Young ?
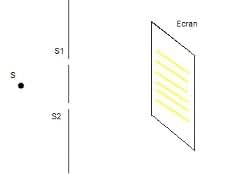
Il s’agit de faire interférer deux faisceaux lumineux issus d’une même source en les faisant passer par deux petits trous comme le montre la figure ci-dessous. La figure d’interférence présente des franges rectilignes.
Dans cette expérience, on suppose que :
- La source S est ponctuelle, monochromatique de longueur d’onde $\lambda$, tout comme les 2 sources secondaires S1 et S2.
- La source S et l’écran sont à très grande distance des trous (conditions de Fraunhofer)
- On ne s’intéresse aux interférences qu’au voisinage du centre de l‘écran.
Source : Par Original téléversé par Pierre 31 sur Wikipédia français. — Pierre CHEVALIER, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=20708102
Comment exprimer l’éclairement ?
D’après la formule de Fresnel, l’éclairement en un point M de l’écran $\mathcal E (M)$ est donné par :
$\mathcal E (M) = 2\mathcal E_0 \left(1+ \cos \left( \frac{2\pi}{\lambda} \delta (M) \right) \right)$
Avec $\delta(M)$ la différence de marche au point M
Dans notre cas, on a :
$\delta (M) = \frac{nax}{D}$
Avec
$n$ l’indice du milieu
$a$ la distance entre les deux trous
$x$ la coordonnée du point M
$D$ la distance des trous à l’écran.
Comment exprimer l’interfrange ?
L’interfrange, noté $i$, est la distance entre deux franges consécutives. D’où :
$p(x+i)=p(x)+1$
Avec $p(x)=\frac{\delta(x)}{\lambda}$ l’ordre d’interférence.
Dans le cas des trous d’Young, l’expression de $i$ :
$i=\frac{\lambda D}{na}$
Que se passe-t-il si la source n’est pas ponctuelle ou pas monochromatique ?
Dans ce cas les interférences sont toujours possibles mais il y a une perte de contraste pouvant aller jusqu’à un brouillage total.