Exercices par compétences corrigés

Établir la convergence d’une suite ou sa divergence vers +∞ ou –∞

Raisonner par récurrence pour établir une propriété d’une suite

Déterminer la limite d’une fonction en un point, en ±∞

Faire le lien entre l’existence d’une asymptote parallèle à un axe et celle de la limite correspondante

Calculer la dérivée d’une fonction donnée par une formule simple

Calculer la fonction dérivée, déterminer les limites et étudier les variations d’une fonction

Lire sur une représentation graphique de 𝑓, de 𝑓’ ou de 𝑓’’ les intervalles où 𝑓 est convexe, concave et les points d’inflexion

Esquisser l’allure de la courbe représentative d’une fonction 𝑓 à partir de la donnée de tableaux de variations de 𝑓, de 𝑓’ ou de 𝑓’’

Démontrer des inégalités en utilisant la convexité d’une fonction

Étudier les solutions d’une équation du type 𝑓(𝑥) = 𝑘 : existence, unicité, encadrement

Pour une fonction continue 𝑓 d’un intervalle dans lui-même, étudier une suite définie par une relation de récurrence 𝑢_{𝑛+1} = 𝑓(𝑢_𝑛)

Utiliser l’équation fonctionnelle de l’exponentielle ou du logarithme pour transformer une écriture, résoudre une équation, une inéquation

Dans le cadre d’une résolution de problèmes, utiliser les propriétés des fonctions exponentielle et logarithme

Savoir résoudre une équation du type cos(𝑥) = 𝑎, une inéquation de la forme cos(𝑥) ⩽ 𝑎 sur [-π, π]

Étudier une fonction simple, définie à partir de fonction trigonométrique, pour déterminer des variations, un optimum

Calculer une primitive en utilisant les primitives de référence et les fonctions de la forme (𝑣’ ∘ 𝑢) × 𝑢’
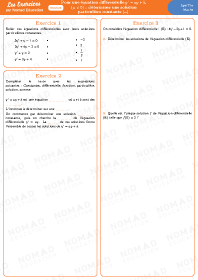
Pour une équation différentielle 𝑦’ = 𝑎𝑦 + 𝑏, (𝑎 ≥ 0) : déterminer une solution particulière constante, utiliser cette solution pour déterminer toutes les solutions

Pour une équation différentielle 𝑦’ = 𝑎𝑦 + 𝑓 : à partir de la donnée d’une solution particulière, déterminer toutes les solutions

Estimer graphiquement ou encadrer une intégrale, une valeur moyenne

Calculer une intégrale à l’aide d’une primitive à l’aide d’une intégration par parties

Majorer (minorer) une intégrale à partir d’une majoration (minoration) d’une fonction par une autre fonction
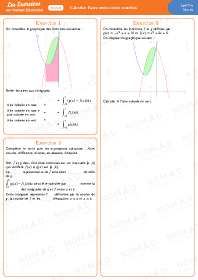
Calculer l’aire entre deux courbes

Étudier une suite d’intégrales, vérifiant éventuellement une relation de récurrence

Interpréter une intégrale, une valeur moyenne


