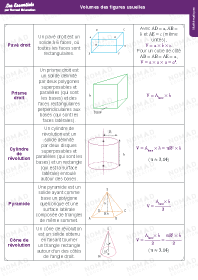
Définition
Une rotation est définie par un point $\rm O$ du plan, qui est le centre de la rotation, et un angle de mesure $\alpha^{\circ}$ ($\alpha$ un nombre positif) avec un sens de rotation.
Le sens des aiguilles d’une montre est appelé sens indirect et son sens inverse, sens direct.
Le point $\rm A’$, qui est l’image d’un point $\rm A$ du plan par cette rotation dont un sens est donné, est tel que :
- $\rm OA’ = OA$ ;
- $\rm \widehat{AOA’} = \alpha^{\circ}$.
Exemple :
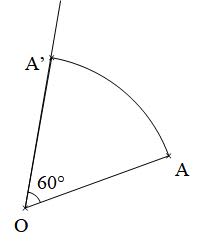
Sur la figure ci-dessous, le point $\rm A’$ est l’image du point $\rm A$ par la rotation de centre $\rm O$ et d’angle $60^{\circ}$ dans le sens inverse des aiguilles d’une montre.
$\rm OA’ = OA$ et $\rm \widehat{AOA’} = 60^{\circ}$.
Pour le placer, on utilise un compas pour tracer un arc de cercle de centre $\rm O$ et de rayon $\rm OA$ (car $\rm OA’ = OA$) et un rapporteur pour tracer la demi-droite $\rm [OA’)$ telle que $\rm \widehat{AOA’} = 60^{\circ}$, dans le sens inverse des aiguilles d’une montre.
Le point $\rm A’$ est situé à l’intersection de l’arc de cercle et de la demi-droite $\rm [OA’)$.
Propriétés
Une rotation :
- conserve les distances : un segment et son image ont même longueur ;
- conserve l’alignement : l’image d’une droite est une droite ;
- conserve les angles : un angle et son image ont même mesure ;
- conserve le parallélisme : les images de deux droites parallèles sont deux droites parallèles.