Définition
On considère une fonction f continue et positive sur l’intervalle [a ;b] (a<b).
On note A l'aire (en unités d’aire) de la surface délimitée par la courbe représentative de f, l'axe des abscisses et les droites d'équation x=a et x=b.
On note ∫baf(x)dx l’aire A.
On a donc A=∫baf(x)dx.
Exemple
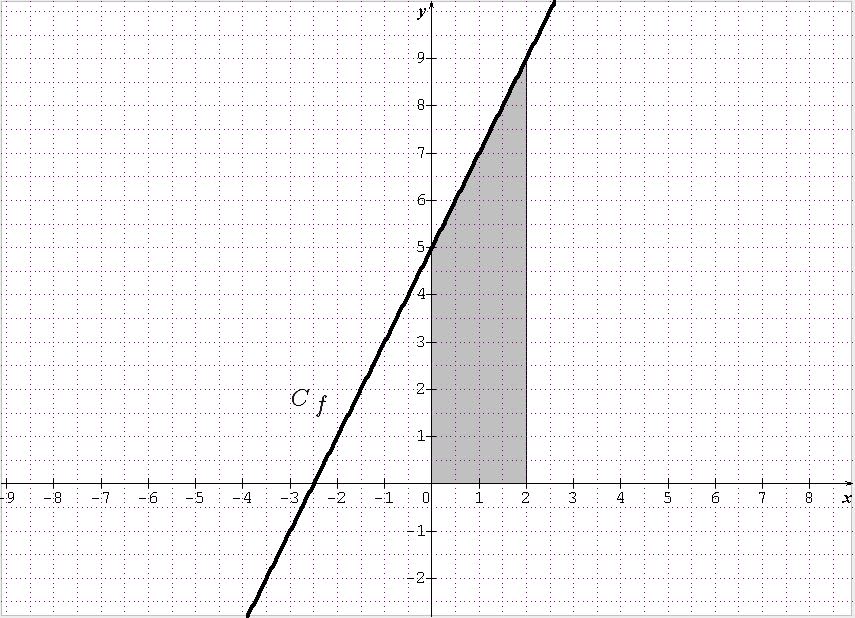
On considère la fonction f définie par f(x)=2x+5 qui est continue et positive sur l’intervalle [0 ;2].
Pour calculer l'aire de la surface délimitée par la courbe représentative de f, l'axe des abscisses et les droites d'équation x=0 et x=2, on utilise les carreaux ou, ici, la formule de l’aire d’un trapèze : (5+9)×22=14.
On a donc ∫20f(x)dx=14 u.a..