Actions sur les solides et grandeurs géométriques des sections de solides

Soient trois vecteurs dont on veut faire la somme et le produit scalaire des deux premiers :

$\overrightarrow{\rm AB}=\left(\begin{array}{cc}a_x\\ a_y\\ a_z\end{array}\right)$ ; $\overrightarrow{\rm BC}=\left(\begin{array}{cc}b_x\\ b_y\\ b_z\end{array}\right)$ ; $\overrightarrow{\rm CD}=\left(\begin{array}{cc}c_x\\ c_y\\ c_z\end{array}\right)$ $\Rightarrow$ $\overrightarrow{\rm AD}=\left(\begin{array}{cc}a_x+b_x+c_x\\
a_y+b_y+c_y \\ a_z+b_z+c_z\end{array}\right)$ et $\overrightarrow{\rm AB}\cdot \overrightarrow{\rm BC} = \rm AB\times BC\times \cos(\overrightarrow{\rm AB}~; \overrightarrow{\rm BC})$ $=(a_x b_x+a_yb_y+a_zb_z)$

Dans un plan $xoy$ :

$\overrightarrow{\rm AB}=\left(\begin{array}{cc}a_x\\
a_y\end{array}\right)$ ; $\overrightarrow{\rm BC}=\left(\begin{array}{cc}b_x\\
b_y\end{array}\right)$ ; $\overrightarrow{\rm CD}=\left(\begin{array}{cc}c_x\\
c_y\end{array}\right)$ $\Rightarrow$ $\overrightarrow{\rm AD}=\left(\begin{array}{cc}a_x+b_x+c_x\\a_y+b_y+c_y\end{array}\right)$

L’unité d’une force est le Newton ou ses multiples.
L’unité de la masse d’un solide est le $\rm kg$ ou ses multiples.
Dans un environnement gravitaire, une masse $\rm (kg)$ génère un poids $\rm (N)$ par la relation :

$\mathrm F=m\times \gamma$.

Sur la terre, la valeur moyenne de l’accélération de la pesanteur est :

$\gamma = g= 9,81~\rm m/s^2$.

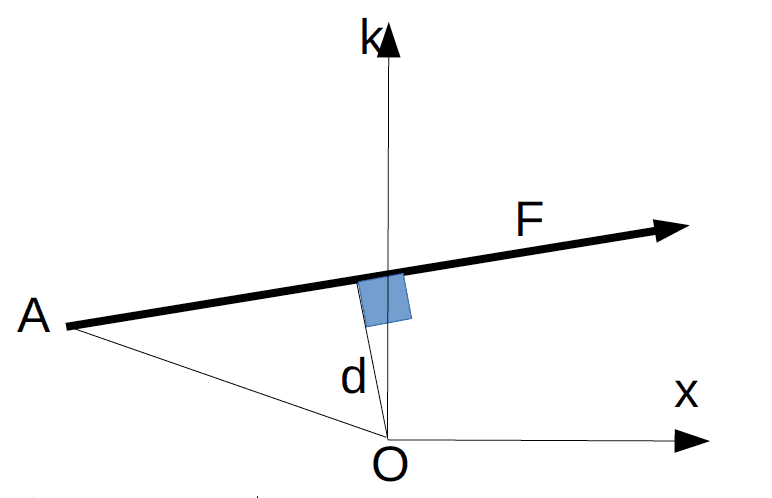
Application du produit vectoriel, moment d’une force en un point :

$\overrightarrow{\rm M_oF}
=\overrightarrow{\rm OA} \wedge \overrightarrow{\rm F}$ $=\| \overrightarrow{\rm OA}\|\times \|\overrightarrow{\rm F}\|\times \sin (\overrightarrow{\rm OA}~; \overrightarrow{\rm F})$ $= \left(\begin{array}{cc}a_x\\
a_y\end{array}\right)\wedge \left(\begin{array}{cc}\mathrm F_x~;
\mathrm F_y\end{array}\right)$ $=(a_x \mathrm F_y−a_y\mathrm F_x)\vec k$

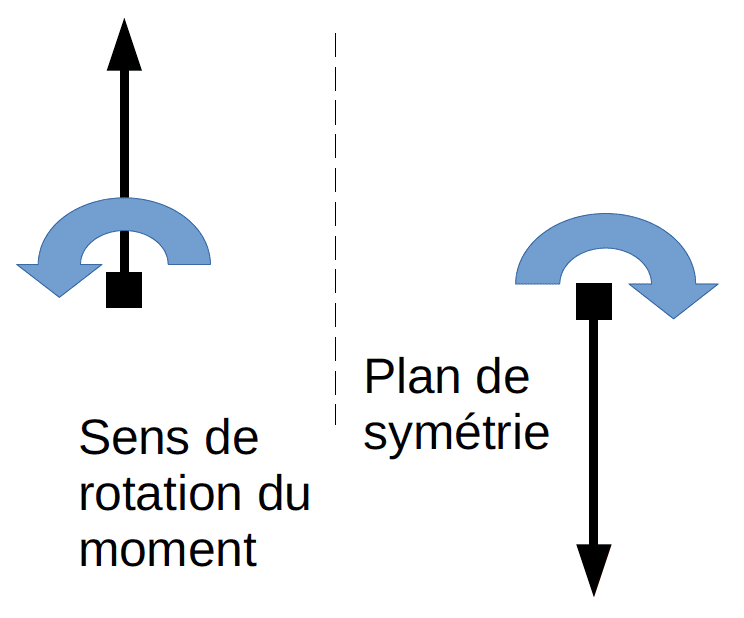
Le symbole $\wedge$ se dit « vectoriel » et définit le produit vectoriel. Le vecteur issu d’un produit vectoriel ne respecte pas les lois de symétrie et donc devient un « pseudo-vecteur » (antisymétrique).

Moment d’une force par le calcul géométrique : $\overrightarrow{\rm M_oF}
=−d\times \| \overrightarrow{\rm F}\| \vec k$ et en appliquant la règle du « tire-bouchon » (ici négatif).

(**) Exemple numérique $\rm \overrightarrow{F}=−500~kN$ sur $y$ ; $d=3,00~\rm m$ sur $x \Rightarrow$ $\rm M_{/o}\overrightarrow{F} =−1~500~m.kN$ sur $z$.

Produit vectoriel dans un système $\rm 3D$ :

$\overrightarrow{\rm AB}=\left(\begin{array}{cc}a_x\\
a_y\\
a_z\end{array}\right)$ ; $\overrightarrow{\rm BC}=\left(\begin{array}{cc}b_x\\ b_y\\ b_z\end{array}\right)$ ; $\Rightarrow$ $\overrightarrow{\rm AB}\wedge \overrightarrow{BC}=\left(\begin{array}{cc}a_x\\a_y\\a_z\end{array}\right)\wedge\left(\begin{array}{cc}b_x\\b_y\\b_z\end{array}\right)$ $=\left(\begin{array}{cc}a_y b_z−b_y a_z\\a_z b_x−b_z a_x\\a_x b_y−b_x a_y\end{array}\right)$

Les indices $(x,y,z)$ ne doivent pas apparaître dans la ligne repérée. Par exemple, la première ligne (axe $x$) n’a pas d’indice $x$.
La première ligne $(x)$ est obtenue en faisant les différences des produits croisés des lignes $(y)$ et $(z)$.
Torseur de force et torseur cinématique : ils sont composés d’une résultante et d’un moment résultant. L’écriture symbolique est :

$\rm T_A=\left[\begin{array}{cc}\overrightarrow{\rm R}\left(\begin{array}{cc}\rm X\\\rm Y\\\rm Z\end{array}\right)\\ \rm \overrightarrow{M_A}\left(\begin{array}{cc}\rm L\\\rm M\\\rm N\end{array}\right)\end{array}\right]$ pour le torseur statique écrit au point $\rm A$ $(\rm R = force$ et $\rm M$ un moment résultant).

$\rm C_A=\left[\begin{array}{cc}
\overrightarrow{\rm \omega}\left(\begin{array}{cc} \omega_x\\
\omega_y\\ \omega_z
\end{array}\right)\\\overrightarrow{\rm V_A}\left(\begin{array}{cc}v_x\\v_y\\v_z\end{array}\right)\end{array}\right]$ pour le torseur cinématique écrit au point $\rm A$ $(\rm V = vitesse$ et $\omega = \text{vitesse de rotation})$

Formules de transfert des moments dans un torseur statique et cinématique :

$\overset{\rightharpoonup}{\rm M_A} = \overset{\rightharpoonup}{\rm M_B} + \overset{\rightharpoonup}{\rm AB} \wedge \overset{\rightharpoonup}{\rm R}$

$\overset{\rightharpoonup}{\rm V_A} = \overset{\rightharpoonup}{\rm V_B} + \overset{\rightharpoonup}{\rm AB} \wedge \overset{\rightharpoonup}{\omega}$

Moment statique d’une section de poutre ou poteau.

$\rm M_S = S\times \cal d_{(\Delta ,x' x)}$ $d$ étant la distance entre l’axe $x’x$ passant par le $\rm CDG$ de $\rm S$ et l’axe $\Delta // x’x$.

On en conclut que le moment statique d’une section de poutre par rapport à un axe passant par son $\rm CDG$ est nul.

En inversant la formule et en généralisant pour plusieurs aires de la section, on en déduit la position du $\rm CDG$ d’une section de forme quelconque :

$\mathrm{Y_G} =
\dfrac{\displaystyle\sum_0^n
\rm M_{S_i}}{\displaystyle\sum_0^n
\rm S_i}$ $=\dfrac{\displaystyle\sum_0^n
\mathrm{S_i}y_{\rm i}}{\displaystyle\sum_0^n\rm S_i}$

Moment quadratique d'une section de poutre ou poteau.

$\mathrm I_\Delta = \displaystyle\int_
{y_1}^{y_2}y_2 d\rm S$

Formule de Huygens : $\mathrm{I_{\Delta}}=\mathrm I_{x 'x}+\mathrm Sd^2$ $d$ étant la distance entre l’axe $x’x$ passant par le $\rm CDG$ de $\rm S$ et l’axe $\Delta // x’x$.

Sections couramment utilisées.

Rectangle plein :

• $\mathrm S=b\times h$
• Centre de gravité $\rm G$ à $\dfrac{b}{2}$ et $\dfrac{h}{2}$
• Moment statique / base : $\mathrm{M_s}=\dfrac{\mathrm Sh}{2}
  = \dfrac{bh^2}{2}$
• Moment quadratique / base : $\mathrm I_{\Delta}=\dfrac{bh^3}{3}$
• Moment quadratique / axe $x ' x$ : $\mathrm I_{x' x}=\dfrac{bh^3}{12}$

Rectangle creux d’épaisseur $\bf e$ :

• $\mathrm S=b\times h−(b−2\mathrm e)\times (h−2\mathrm e)$
  Centre de gravité $\rm G$ à $\dfrac{b}{2}$ et $\dfrac{h}{2}$
• Moment statique / base : $\mathrm{M_s}=\dfrac{bh^2}{2}−(b−2\mathrm e)(h−2\mathrm e)\dfrac{h}{2}$
• Moment quadratique / axe $x ' x$ : $\mathrm I_{x' x} = \dfrac{1}{12} \times \left[bh^3−(b−2\mathrm e)(h−2\rm e)^3\right]$

Triangle plein :

• $\mathrm S=\dfrac{bh}{2}$
• Axe $x ' x$ positionné au $\dfrac{1}{3}$ de la hauteur
• Moment statique / base : $\mathrm{Ms}=\dfrac{bh^2}{6}$
• Moment quadratique / $x ' x = \mathrm I_{x ' x} = \dfrac{bh^3}{36}$
• Moment quadratique / $y ' y : \mathrm I_{y ' y} = \dfrac{b^3h}{48}$

Cercle plein de diamètre $\bf D$ :

• Surface : $\rm S=\pi\dfrac{D^2}{4}$
• Moments quadratiques : $\mathrm M_{y ' y} = \mathrm M_{x ' x} =\pi \dfrac{\rm D^4}{64}$
• Moment quadratique polaire : $\mathrm{M_o}=\mathrm M_{x' x}+\mathrm M_{y ' y} = \pi\dfrac{\rm D^4}{32}$

Cercle creux de diamètres $\bf D_{extérieur}$ et $\bf d_{intérieur}$ :

• Surface : $\rm S=\dfrac{\pi}{4}(D^2−\mathcal d^2)$
• Moments quadratiques : $\mathrm M_{y ' y}=\mathrm M_{x ' x}=\dfrac{\pi}{64}(\mathrm D_4−d_4)$
• Moment quadratique polaire : $\rm M_o=\dfrac{\pi}{32} (D^4−\mathcal d^4)$

Ellipse pleine de diamètres $\bf D=2a$ et $\bf d=2b$ :

• $\mathrm S=\pi ab=\dfrac{\pi}{4}\mathrm Dd$
• Moment quadratique selon $x ' x$ : $\mathrm I_{x' x}=\dfrac{\pi}{4}ab^3$
• Moment quadratique selon $y ' y=\mathrm I_{y 'y}=\dfrac{\pi}{4}ba^3$