$\boxed{\rm \sigma=E~\varepsilon}$ avec : $\rm E =$ module d’élasticité longitudinale ou module d’Young $(>0)$ et $\varepsilon$ la déformation relative de la fibre repérée.
La contrainte $\sigma$ est donc du même signe que la déformation relative.
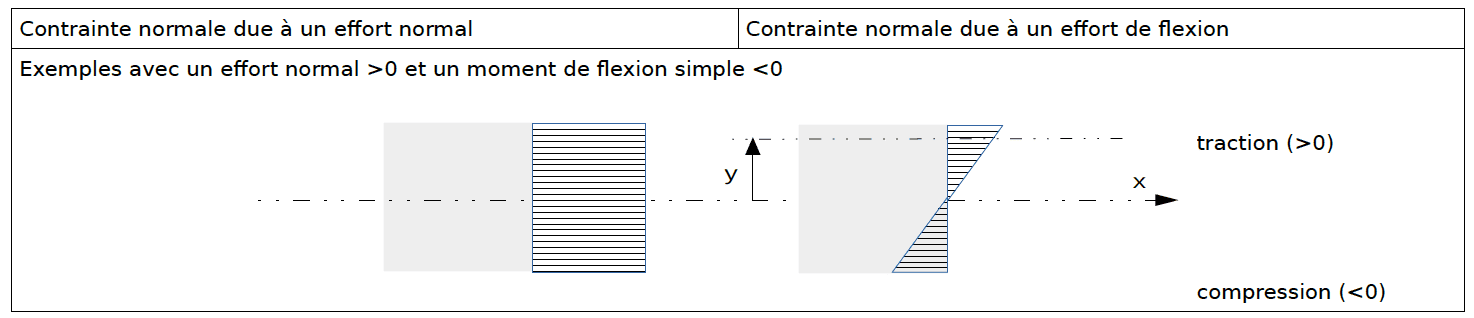
Contraintes internes et déformations
$\boxed{\rm \sigma=E~\varepsilon}$ avec : $\rm E =$ module d’élasticité longitudinale ou module d’Young $(>0)$ et $\varepsilon$ la déformation relative de la fibre repérée.
La contrainte $\sigma$ est donc du même signe que la déformation relative.

Les conventions de signe sont issues des convention mathématiques.
| $\rm \sigma = \dfrac{N}{S}$ ; $\rm \sigma=−\dfrac{M}{I} \mathcal y$ ; $\sigma$ en $\rm Mpa(MN/m^2$ ou $\rm N/mm^2)$ |
Expression de la contrainte tangentielle en fonction de l’effort tranchant $\mathrm V(x)$ :
$\boxed{\tau=\dfrac{\mathrm V_{(x)} \mathrm M_s}{\mathrm I_{x’ x}b_{(y)}}}$
$\rm M_s =$ moment statique de la partie de section au-dessus de la position de $y$.
$\mathrm I_{x’x} =$ moment quadratique de la section de poutre par rapport à l’axe du $\rm CDG$.
$b_{(y)} =$ largeur de la section de poutre au niveau de la cote $y$.
Expression de la contrainte tangentielle liée au moment de torsion :
$\boxed{\tau =\dfrac{r_{\rm C}}{\rm I_0}}$
$r =$ rayon du cylindre circulaire.
$\rm C =$ couple (moment) selon l’axe de la poutre en général cylindrique.
$\rm I_0 =$ moment quadratique polaire de la poutre cylindrique valant $\boxed{\rm I_0= \dfrac{\pi D^4}{32}}$.
Expression de la contrainte normale liée à une flexion composée (flexion simple selon $z$ et effort normal selon $x$) :
$\boxed{\sigma = \mathrm{\dfrac{N}{S}} − \dfrac{\mathrm M_z}{\mathrm I_z} \times y}$
Expression de la contrainte normale liée à une flexion composée (flexion déviée selon $y$ et $z$, effort normal selon $x$) :
$\boxed{\sigma =\dfrac{\rm N}{\rm S} − \dfrac{\mathrm M_z}{\mathrm I_z} \times y + \dfrac{\mathrm M_y}{\mathrm I_y} \times z}$
Expression de la déformation planaire de poutres. Relation entre la courbure et le moment fléchissant. Si :
Alors on a : $\boxed{\dfrac{\mathrm M_{(x)}}{\mathrm{EI}_{z ’ z}} = \dfrac{1}{r} = \dfrac{y_x^{’’}}{[1+ y_x^{’2}]^{\frac{3}{2}}} \approx y_x^{’’}}$ puis on procède par $2$ intégrations successives pour obtenir la flèche $y$.
Sauf dans le cas où l’on étudie une poutre travaillant en Cexion pure (appelée encore Cexion circulaire), la formule approchée suGt amplement, car la pente est très faible.


