Poutres en acier, comportement vis à vis de la flexion simple

Exemple de vérification d’une poutre en acier, articulée à gauche et sur appui simple à droite, de portée $\rm L = 10,00~m$. Le chargement est uniformément réparti. Cette poutre est intégrée dans une toiture industrielle. Les valeur des produits sont extraits du catalogue Arcelor (zone jaune clair).

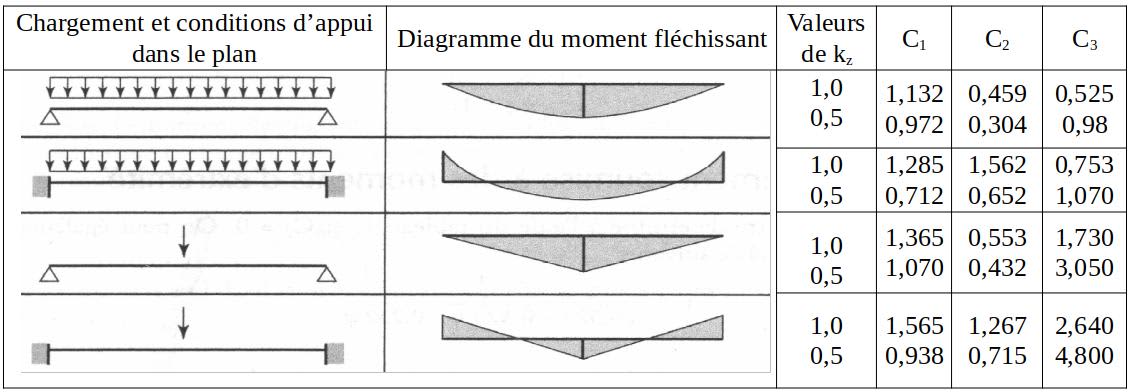
Évaluation des moment fléchissants. La RDM nous dit que :

$\mathrm M = \dfrac{pl^2}{8}$ ; $\mathrm V = \dfrac{pl}{2}$ ainsi que $\sigma = \rm \dfrac{M}{\frac{I}{\mathcal v}}$ pour les fibres extrêmes tendues ou comprimées. La flèche centrale vaut : $f = \dfrac{5pl^4}{384 \rm EI}$

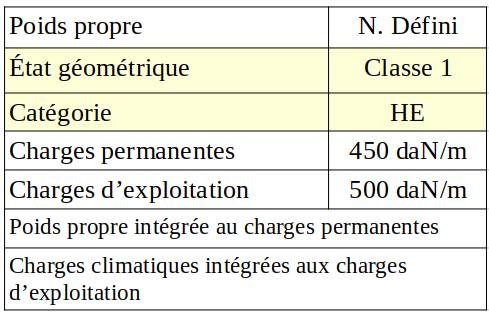
$\rm G=450~daN / m = 4,5~kN /m$ et $\rm Q=500~ daN /m = 5~kN / m$
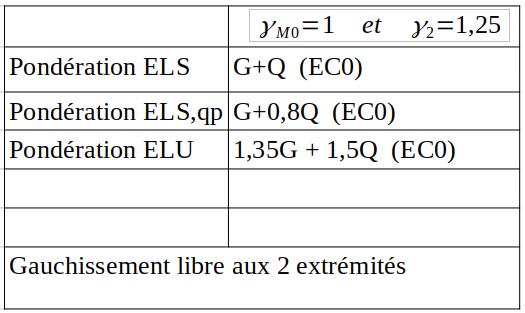
$\Rightarrow p_{\rm ELS} = \rm 9,5~ kN / m$ ; $p_{\mathrm{ELS},qp} = \rm 8,5~kN / m$ ; $p_{\rm ELU} = \rm 13,58~kN /m$

$\mathrm M_{se} = 118,75~\rm m. kN$ ; $\mathrm M_{se ,qp} = 106,25~\rm m.kN$ ; $\mathrm M_u = \rm M_{ED} = 169,75~m.kN$
$\mathrm V_{se} = \rm 47,5~kN$ ; $\mathrm V_{se, qp} = 42,5~\rm kN$ ; $\rm V_{ED} = 67,9~kN$

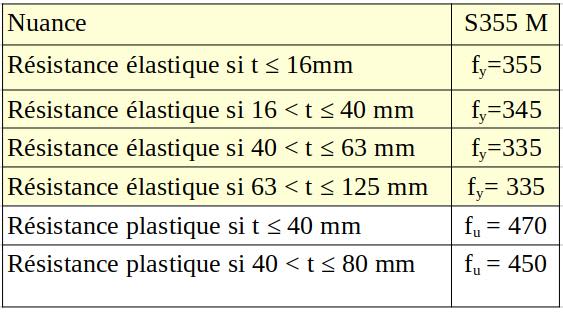
Situation à étudier car nous sommes en classe 1, mode plastique $\mathrm{M_{ED}} \leq \mathrm M_{\mathrm C,Rd} = \mathrm M_{pl, Rd} = \dfrac{\mathrm W_{pl}f_y}{\gamma_{\rm M0}}$ $\Rightarrow \mathrm W_{pl} \geq \dfrac{\mathrm M_{pl,rd} \times \gamma_{M0}}{f_y}$ en égalisant le moment ultime $\rm M_{ED}$ au moment plastique $\mathrm M_{pl,Rd}$ (situation limite) en supposant un profilé de taille moyenne avec $f_y = 335~\rm MPa$.

$\mathrm W_{pl} \geq \dfrac{0,16975 \times 1}{335} = \rm 0,000507~m^3=507~ cm^3$ soit par exemple un $\rm HE220A$. Il s’agit d’un petit profilé avec $f_y = 355~\rm MPa$, ce qui permettrait d’affiner à la baisse le type de profilé, ce que nous ne ferons pas à cause de la déformée.

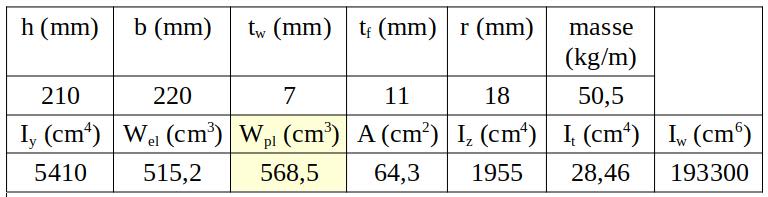
En vérification ELS, mode élastique, nous aurons avec $f_y = 355~MPa$ :

$\mathrm M_{se} \leq \mathrm M_{\mathrm C, Rd} = \mathrm M_{el, Rd} = \dfrac{\mathrm W_{ef}f_y}{\gamma_{\rm M0}}$ $\Rightarrow \mathrm W_{el} \geq \dfrac{\mathrm M_{el, Rd} \times \gamma_{\rm M0}}{f_y}$ soit par exemple un $\rm HE200A$.
$\mathrm W_{el} = \dfrac{0,11875\times 1}{355} = \rm 0,000335~m^3 = 335~cm^3$.

Mais il faut vérifier la flèche réelle avec la flèche admissible, ainci que les risques de voilement (on conservera la première solution).

$f = \dfrac{4p_{\mathrm{ELS}, qp}l^4}{\rm 384 EI}$ $= \dfrac{5 \times 8,5\cdot 10^{-3} \times 10^4}{384 \times 2~100~000 \times 0,00005410}$
$f = \rm 0,098~m > \dfrac{\mathcal l}{500}$ $= \dfrac{10}{500}$ $\rm = 0,02~m$ $\rm= 2~cm$

Remarque : Comme il y a une portée importante de $\rm 10,00~m$ avec un chargement modéré, c’est la déformée qui prédomine et non la résistance de la poutre. Vérification au cisaillement. Calcul plastique.

$\mathrm A_v = \mathrm{Max}[\mathrm A - 2bt_f + (t_w + 2r)t_f~;h_wt_w$
$\mathrm A_v = \rm Max(20,575~cm^2~;14~cm^2)$ $\rm = 20,575~cm^2$

$\mathrm V_{c,Rd} = \mathrm A_v \left(\dfrac{f_y}{\gamma_{\rm M0}\sqrt 3}\right)$ $= 20,575\cdot 10^{−4}\left(\dfrac{355}{1\times \sqrt 3}\right)$ $=0,421~\rm MN$
$\mathrm V_{c, Rd} > \rm V_{ED} = 67,9\cdot 10^{−3}~MN \Rightarrow OK$

Vérification du risque de voilement de l’âme au droit des appuis.

$\varepsilon = \sqrt{\dfrac{235}{f_y}} = \sqrt{\dfrac{235}{355}} = 0,813$

$\Rightarrow$ Si $\dfrac{h_w}{t_h} = \dfrac{200}{7} = 28,57 > ~? ~72 \dfrac{\varepsilon}{\eta}$ $= \dfrac{72\times 0,813}{1,2}=48,78$

$\rm \Rightarrow NON \Rightarrow$ pas de renforcement de l'âme.

Vérification du risque de déversement. Poutres symétriques.
Si les moments aux extrémités sont différents $\rm M_1 \geq M_2 = \Psi M_1$ avec $−1\leq \Psi \leq+1$ et/ou la sollicitation en flexion simple, alors :

$\mathrm M_{cr} = C_1 \times π^2 \dfrac{\rm EI}{(k_z\rm L)^2}$ $\scriptstyle\left[\sqrt{\left(\frac{k_z}{k_w}\right)^2\times \frac{\mathrm I_w}{\mathrm I_z} + (k_z\mathrm L)^2 \times \left(\frac{\mathrm{GI}_t}{\pi^2\mathrm{EI}_z}\right) + (\mathrm C_2 z_g − \mathrm C_3 z_j)^2} − (\mathrm C_2 z_g − \mathrm C_3 z_j)\right]$

Avec :

Moment d’inertie de gauchissement $(\rm m^6, cm^6$ ou $\rm mm^6)$ $\mathrm I_w = \beta (1−\beta)$ $\mathrm I_z h_s^2$ avec $\beta_f = \dfrac{\mathrm I_{f_c}}{\mathrm I_{f_c}\mathrm I_{f_t}}$

• $h_s =$ distance entre les centres de torsion/cisaillement des semelles sup. et inf. $(h - t_f)$.
  Les centres de torsion/cisaillement des semelles sont sont à la demi épaisseur de celles-ci.
• $\mathrm I_{f_c} =$ moment quadratique de la semelle comprimée.
• $\mathrm I_{f_t} =$ moment quadratique de la semelle tendue
  Pour une section rectangulaire pleine, le centre de torsion est confondu avec le CDG.
• $z_g =$ distance du point d’application de la charge au centre de torsion (différent du CDG et signe + si la charge agit vers le centre de torsion).

$z_g=z_a−z_s$ avec $z_s =$ coordonnées du centre de torsion et $z_a =$ coordonnées du point d’application de la charge.

Pour une section symétrique $\rightarrow z_j = z_s - \left[\dfrac{0,5}{\mathrm I_y} \times \displaystyle \int_{\rm A} z (y^2 + z^2) d\mathrm A\right] = 0$ si elle est doublement symétrique (mêmes semelles en haut et en bas, $\rm H$ ou $\rm I$).

Dans ce cas, nous aurons : $\beta_f = \dfrac{\mathrm I_{f_c}}{\mathrm I_{f_c}\mathrm I_{f_t}} = 0,5$ $\Rightarrow$ $\mathrm I_w=\beta (1−\beta) \mathrm I_z h_s^2 = \dfrac{\mathrm I_z}{4} \times (h - t_f)^2$

Si $k_z=k_w=1 \Rightarrow \rm C_1$ $= \dfrac{1}{\sqrt{(0,325+0,423\Psi+0,252\Psi^2)}} \leq 2,6$ uniquement pour les moments d’extrémité $\rm (C_2 = C_3 = 0)$.

Facteurs réducteurs de la longueur de déversement :

Dans le cas général, il convient de consulter les tableaux F.1.1
(moments d’extrémité) et F.1.2
(chargement en travée) de l’EC3 pour avoir les valeurs de $\rm C_1$ (lié aux aux moments d’extrémité), $\rm C_2$ (lié à la position de la charge) et $\rm C_3$ (lié à la liaison latérale).
Pour notre exemple, $\rm C_1 = 1,132, C_2 = 0,459, C_3$ inutile, car $z_j = 0$, $z_g = 105~\rm mm$, $k_w = k_z = 1$.

Et $\scriptstyle\mathrm M_{cr} = \mathrm C_1\times \pi^2 \frac{\mathrm{EI}_z}{(L)^2}\left[\sqrt{\frac{\mathrm I_w}{I_z} + \mathrm L^2 \times \left(\frac{\mathrm{GI}_t}{\pi^2\mathrm{EI}_z}\right) + (\mathrm C_2 z_g)^2} − (\mathrm C_2 z_g)\right]$ avec $\rm G = \dfrac{E}{2(1+ \mathcal v)} = 80 770~MPa$.

$\scriptstyle \mathrm M_{cr} = 1,132\times \frac{\pi^2 \times 210~000\times 1~955\cdot 10^{−8}}{10^2} \times$ $\scriptstyle\left[\sqrt{\frac{0,1933\cdot 10^{-6}}{1~955\cdot 10^{-8}} + \frac{10^2\times 8~0770\times 28,46\cdot 10^{−8}}{\pi^2 \times 210~000 \times 1~955\cdot 10^{−8}} + (0,459\times 0,105)^2}\right.$ $\scriptstyle − 0,459\times 0,105\big]$

$\rm M_{ED} = 0,16975~m. MN > M_{\cal cr}=0,098~ m. MN \rightarrow$ risque de déversement.

Encastrement bidirectionnel : $k_z = k_w = 0,5$

$\scriptstyle \mathrm M_{cr} = \rm C_1\times \pi^2 \frac{\mathrm{EI_z}}{\rm 0,5L)^2}\left[\sqrt{\frac{\mathrm I_w}{\mathrm I_z} + L^2 \times \left(\frac{\mathrm{GI_t}}{\pi^2 \mathrm{eI}_z}\right) + (\mathrm C_2 z_g)^2} − (\mathrm C_2 z_g)\right]$ ce qui multiplie par $4$ le moment critique $\rightarrow \mathrm M_{cr} = \rm 0,392~m.MN > M_{ED} \rightarrow OK$

Dans le cas d’une réalisation « sur mesure » on peut avoir besoin des expressions des critères géométriques de dimensionnement pour des section $\rm H$ ou $\rm I$ (extrait du catalogue Arcelor). Aire de la section transversale (unités usuelles en $\rm m^2$, $\rm cm^2$ ou $\rm mm^2$). $\mathrm A = 2t_f b +(h−2t_f)\times t_w + (4−\pi) \times r^2$

Moments quadratiques de flexion. (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$)
$\mathrm I_y = \dfrac{1}{12} \times [bh^3 −(b−t_w)\times (h−2 t_f)^3]$ $+$ $0,03 r^4 + 0,2146 r^2 (h−2t_f−0,4468r)^2$
$\mathrm I_y = \dfrac{1}{12} \times [2t_f b^3 +( h−2t_f) t_w^3] + 0,03r^4$ $+$ $0,2146 r^2 (t_w + 0,4468 r)^2$

Module de flexion plastique (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$) : $\mathrm W_{pl, y} = t_w\dfrac{h^2}{4} + (b−t_w) (h − t_f) t_f$ $+$ $\left(\dfrac{4−\pi}{2}\right)r^2(h−2t_f)+\left(\dfrac{3\pi^−10}{3}\right)r^3$

Modules de flexion élastique (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$) : $\mathrm W_{el, y} = 2\dfrac{\mathrm I_y}{h}$ et $\mathrm W_{el, z} = 2\dfrac{\mathrm I_z}{b}$

Moment quadratique de torsion (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$)
$\mathrm I_t = \dfrac{2}{3} \times (b−0,63t_f)\times t_f^3 + \dfrac{1}{3}\times (h−2t_f)\times t^3_w + 2 \times \left(\dfrac{t_w}{t_f}\right)$ $\times$ $\left(0,145+0,1\times \dfrac{r}{t_f}\right)$ $\times$ $\left[ \dfrac{\left(r + \frac{t_w}{2}\right)^2 +(r+t_f)^2}{2r+t_f}\right]^4$