Quand un rayon est réfléchi par une surface, il est renvoyé dans même plan que le rayon incident. Ainsi nous avons l’angle du rayon réfléchi par rapport à la normale qui est égal à celui du rayon incident par rapport à la normale : $i = r$.

Quand un rayon est réfléchi par une surface, il est renvoyé dans même plan que le rayon incident. Ainsi nous avons l’angle du rayon réfléchi par rapport à la normale qui est égal à celui du rayon incident par rapport à la normale : $i = r$.

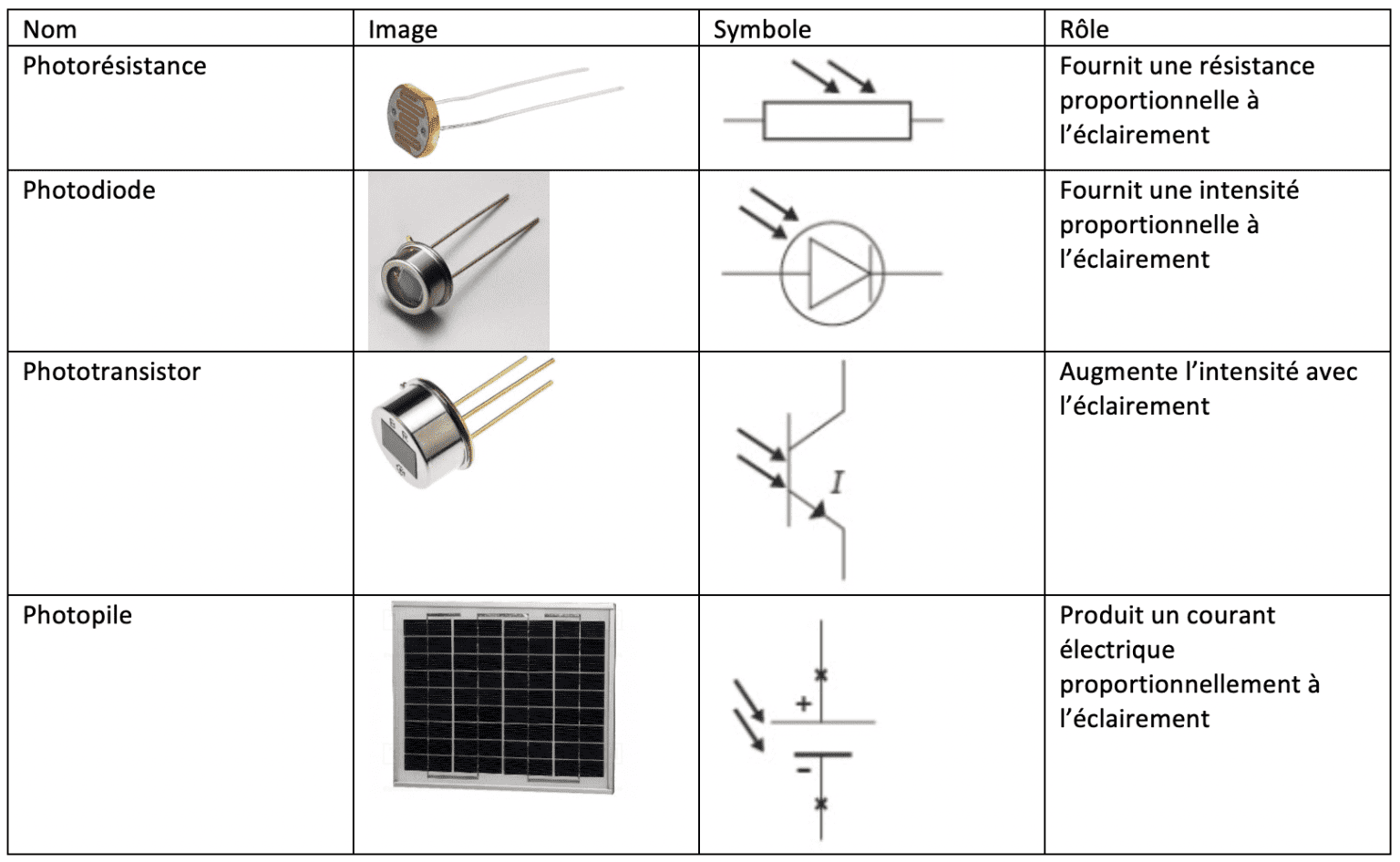
Lorsqu’un rayon lumineux traverse une surface (par exemple il arrive par l’air et passe dans l’eau), il est dévié par le milieu. Nous avons $n_1 \sin (i_1) = n_2 \sin (i_2)$.
$n_1$ et $n_2$ sont les indices de réfraction des milieux considérés. Plus l’indice augmente, plus le milieu sera dit « réfringent » et plus le rayon sera dévié par rapport à la normale.
Si $n_2 > n_1$, à partir d’un certain « angle limite », les rayons ne seront plus réfractés mais seulement réfléchis. C’est ce qu’on appelle une réflexion totale.
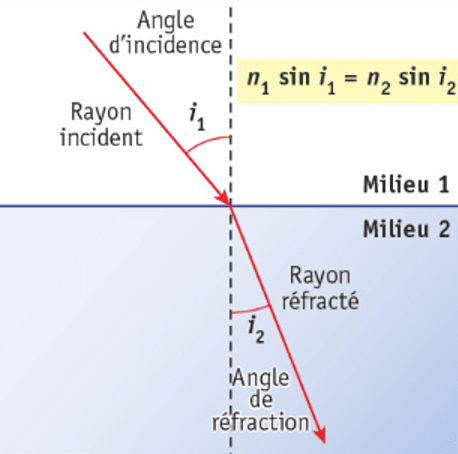
La lumière de couleur blanche est en fait le mélange de toutes les couleurs. Quand cette lumière est décomposée, nous obtenons le spectre continu de la lumière blanche.
Chaque couleur, ou rayonnement monochromatique qui compose la lumière blanche, possède une longueur d’onde $\lambda$ unique, exprimée en mètres $\rm (m)$ qui la caractérise.
Les longueurs d’onde visibles sont celles comprises entre $\rm 400~ nm$ et $\rm 800~ nm$. Les $\rm UV$, invisibles, ont une longueur d’onde inférieure à $\rm 400~ nm$. Les $\rm IR$ (infra-rouges) ont une longueur d’onde supérieure à $\rm 800~ nm$.
La lumière étant une onde électromagnétique se propageant à la vitesse de la lumière, elle possède une fréquence f (en Hertz, $\rm Hz$), donnée par :
$\displaystyle\rm \lambda=\frac{c}{f}$
Avec $\rm c$, la célérité ou vitesse de la lumière, $\rm c = 3 \cdot 10^8~ m/s$.
La lumière est une onde électromagnétique, mais est également composée de particules appelées photons. Ils ont une énergie différente pour chaque longueur d’onde :
$\displaystyle \rm E = h \times \frac{c}{\lambda}$ avec $\rm E$ l’énergie du photon en Joules $\rm (J)$, $\rm c$ la célérité en $\rm m/s$ et $\lambda$ la longueur d’onde en $\rm m$ ; $\rm h$ est la constante de Planck, avec $\rm h=6,62 \times 10^{-34}~J.s$.
En lumière, les couleurs primaires sont Rouge, Vert et Bleu. Il est possible d’obtenir les autres couleurs par superposition (comme pour un mélange en peinture). Si elles sont toutes superposées, nous obtenons une lumière blanche.

Si nous utilisons des filtres colorés devant une lumière colorée, nous obtenons les mêmes mélanges qu’en peinture : si tous les filtres des couleurs primaires sont superposés, plus aucune couleur ne les traverse et nous n’avons plus de lumière. C’est le noir absolu.

Les objets de couleurs absorbent certaines couleurs et diffusent les autres (ce sont celles qu’on voit). Il faut se baser sur la synthèse additive des couleurs pour le savoir.
Exemple : une banane jaune a en fait absorbé tout le bleu de la lumière blanche, et a diffusé les couleurs rouge et vert, comme le jaune est constitué de rouge et de vert en lumière. Si elle est éclairée en cyan, elle paraîtra verte et si elle est éclairée en bleu, elle paraîtra noire.

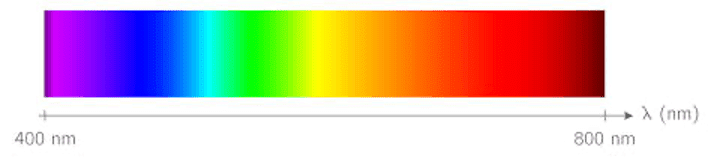
Les photo-composants reposent sur l’effet photoélectrique. C’est la capacité qu’ont certains matériaux à libérer des électrons sous l’action d’une onde électromagnétique. C’est le cas des cellules photovoltaïques d’un panneau solaire qui sont un assemblage de photopiles.
La puissance totale d’un rayonnement électromagnétique (d’une lumière) est notée : $\rm \Phi_E$. C’est le flux énergétique total, exprimé en Watts $\rm (W)$.
La puissance lumineuse perçue par l’œil est mesurée en lumen (lm) et est notée $\rm \Phi_V$. Elle peut se calculer de la manière suivante :
$\rm \Phi_V = E \times S$ avec $\rm E$ l’éclairement mesuré avec un luxmètre en lux et $\rm S$ la surface éclairée en $\rm m^2$.
L’efficacité lumineuse d’une source est donc :
$\displaystyle\rm K_S = \frac{\Phi_V}{\Phi_E}$
Les photo-composants les plus courants sont les suivants :