Réaliser des circuits électriques simples et exploiter les lois de l’électricité

Exploitation des lois de l’électricité et étude de quelques circuits électriques simples

Le courant électrique est la manifestation d’un transfert d’énergie par déplacements de porteurs de charges électriques : les électrons. Si ces électrons se déplacent entre deux bornes d’un appareil électrique (dipôle), il existe une tension électrique non nulle.

La quasi-totalité de nos appareils domestiques utilise cette forme d’énergie pour fonctionner.

Pour fonctionner, un appareil électrique doit être branché dans un circuit électrique fermé, relié à un générateur électrique et à un coupe-circuit pour assurer la sécurité de l’installation.

• Dipôles en série

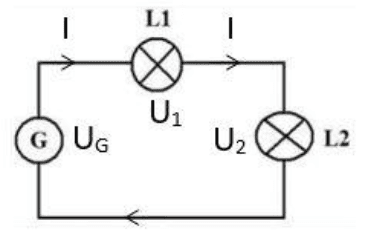
Dans une configuration en série, les éléments du circuit sont disposés les uns après les autres, formant une seule boucle, appelée "maille".

Dans cet exemple, un générateur (pile) alimente deux lampes.

1. L’intensité I du courant est la même en tout point du circuit : c’est la loi d’unicité de l’intensité.
2. La somme des tensions aux bornes des lampes est égale à la tension fournie par le générateur. C’est la loi d’additivité des tensions. $\rm U_1 + U_2 = U_G$

• Dipôles en dérivation

Dans une configuration en dérivation, les éléments du circuit sont disposés en parallèle les uns aux autres, formant plusieurs boucles.

Dans cet exemple, un générateur (pile) alimente deux lampes.
Le courant d’intensité I issu du générateur bifurque dans la lampe $\rm L_1$ et dans la lampe $\rm L_2$ : $\rm I = I_1 + I_2$. C’est la loi d’additivité des intensités.

• Relation tension-courant : loi d’Ohm

Il existe une relation de proportionnalité entre l’intensité I du courant parcourant un conducteur ohmique, sa résistance R et la tension U à ses bornes : $\rm U = R \times I$

Avec U en volt (V), R en ohm (Ω) et I en ampère (A)

Dans la vie courante, la consommation d’électricité d’une habitation est proportionnelle à l’énergie électrique consommée.

Cependant la facture n’est pas exprimée en Joules, mais en kWh (prononcer kilo Watt heure). Cette unité est également une unité d’énergie.

Ensuite, cette quantité, lue au niveau du compteur, est multipliée par le coût d’un kWh pour pouvoir établir la facture.

Attention : pour un compteur heures creuses, heures pleines, il y aura la quantité d’énergie électrique consommée pour chaque période à prendre en compte, ainsi que le coût de l’énergie électrique de chaque période.

Pour les calculs, on rappelle que : $\rm P = 𝐸~ /~ \Delta𝑡$

Avec la puissance en W, l’énergie en kWh et le temps en h.

La puissance caractérise la capacité d’un appareil à libérer rapidement de l’énergie.

La puissance électrique P d’un appareil correspond au produit de la tension électrique U à ses bornes par l’intensité du courant électrique I qui le traverse :

$\rm P = U \times I$

Avec P en watt (W), U en volt (V) et I en ampère (A).

L’énergie électrique E consommée par un appareil correspond au produit de sa puissance P par sa durée de fonctionnement t : $\rm E = P \times \Delta t$

$\rm E$ en joule (J), $\rm P$ en watt (W) et $\Delta t$ en seconde (s).

Nous avons précédemment vu que $\rm P = U \times I$

D’où $\rm E= U \times I \times \Delta t$

Avec $\rm U$ en volt et $\rm I$ en ampère.

Remarque :

Un joule correspond au produit d’un watt par une seconde : $\rm 1 ~J = 1~ W/s$

Si le temps est exprimé en heure (h), alors l’énergie s’exprime en wattheure (Wh). Le wattheure correspond au produit d’un watt par une heure :

$\rm 1~ Wh = 1 \times 3 ~600 = 3~ 600 = 3~ 600 ~J$

Pour calculer la consommation électrique des foyers en France, les fournisseurs d’électricité utilisent des compteurs électriques qui mesurent l’énergie électrique, en kilowattheure (kWh) :

$\rm 1~ kWh = 1 ~000 ~Wh$
$\rm = 1 000 \times 3 ~600 = 3 ~600 ~000 ~J$