Tout comprendre sur les identités remarquables 🔢
Ah, les identités remarquables... Rien que le nom peut intimider ! Mais pas de panique, nous allons démystifier ensemble ces formules qui, une fois maîtrisées, te feront gagner un temps précieux dans tes calculs. Que tu sois en classe de troisième ou au lycée, cette leçon est faite pour toi !
Qu’est-ce qu’une identité remarquable ?
Une identité remarquable est une équation qui est toujours vraie, quel que soit le nombre que l'on met dans l'équation. Autrement dit, ce sont des formules magiques qui simplifient nos calculs. Apprendre ces identités par cœur permet de résoudre des équations plus facilement et plus rapidement.
Les trois identités remarquables à connaître sont :
- Le carré d'une somme : (a+b)² = a²+ 2ab + b²
- Le carré d'une différence : (a−b)² = a²− 2ab + b²
- Le produit de la somme par la différence : (a+b)(a−b) = a² − b²
Ces formules sont omniprésentes en mathématiques et seront tes alliées tout au long de tes études. Tu dois ABSOLUMENT les connaître par cœur !! Voyons ensemble comment les utiliser efficacement !
Le carré d'une somme
Imagine que tu doives développer l'expression (x+5)²(x + 5)² (x+5)².
Plutôt que de multiplier (x+5)(x + 5)(x+5) par lui-même, utilise la formule du carré d’une somme :
Hop ! En un clin d'œil, tu as développé l'expression sans avoir à tout recalculer manuellement. Tu vois, c'est simple comme bonjour ! 😎
Le carré d'une différence
Pas de jaloux, la même logique s'applique au carré d'une différence ! Prenons (x−3)².
Utilisez la formule suivante :
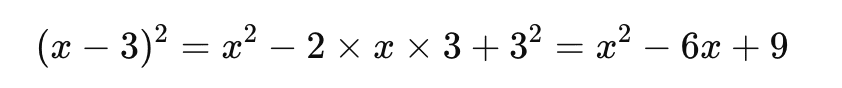
Encore une fois, pas besoin de se perdre dans les calculs, la formule fait tout le travail pour toi.
Le produit de la somme par la différence
Dernière formule, mais pas des moindres : le produit de la somme par la différence. Elle te permet de transformer un produit en somme.
Par exemple :
En un tour de main, l'expression est simplifiée ! 🪄
Pourquoi apprendre ces identités ?
Les identités remarquables sont partout ! En plus de simplifier les calculs, elles te seront indispensables pour résoudre des équations complexes, factoriser des expressions, et même en géométrie analytique. Leur utilisation régulière te permettra de les maîtriser jusqu’à ce qu’elles deviennent une seconde nature.
💡 Un conseil : entraîne-toi !
Comme pour tout, la clé est la pratique. N'hésite pas à utiliser ces formules à chaque occasion. Une fois que tu les auras bien en tête, elles te feront gagner un temps précieux lors de tes examens.
Exercice pratique :
Factorise l’expression suivante : x² + 10x +25x² + 10x + 25.
Si tu as bien suivi, tu as alors trouvé que cela peut être réécrit comme (x + 5)².
Bravo, tu as utilisé une identité remarquable ! ✅
Pour approfondir tes connaissances sur les identités remarquables, retrouve dans ton application Nomad Education, tout ce qu'il faut pour consolider tes acquis et t'entraîner à développer et factoriser grâce aux identités remarquables.
- Des mini-cours complets sur les identités remarquables
- Des quiz pour te tester sur les formules des identités remarquables
- Des exercices pas à pas corrigés pour t'entraîner
- Des fiches de révisions de maths sur les identités remarquables
- Des vidéos explicatives sur les identités remarquables
En maîtrisant ces trois formules incontournables des identités remarquables, tu te donnes les moyens de réussir en maths.
éeAlors, prêt à relever le défi ? 🚀
#identitésremarquables #identitéremarquable #formules #mathématiques #maths #exercices #coursidentitésremarquables #coursdemaths #quizmaths #fichesmaths #lycée #profdemaths #notionmaths #nomadeducation #équations
