Puissances
📝 Mini-cours GRATUIT
Puissance d’un nombre non nul
🍀 Fiches de révision PREMIUM

Transformations géométriques

Théorèmes et propriétés de géométrie
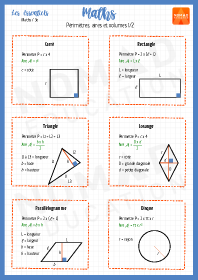
Périmètres, aires et volumes

Fonctions linéaires et affines

Nombres et Calculs

Statistiques et probabilités

Calcul littéral et équations
🎲 Quiz GRATUIT
📄 Prépare ton éval PREMIUM

Puissances
📄 Annales PREMIUM

Annales 2021 Centres étrangers 1 (Mathématiques 3ème)

Annales 2018 Métropole

Annales 2021 Métropole (Mathématiques 3ème)

Annales 2016 Métropole

Annales 2019 Métropole

Annales 2021 Centres étrangers 2 (Mathématiques 3ème)

Annales corrigées de Maths – Métropole 2022

Annales corrigées de Maths – Métropole 2023

Annales Mathématiques Série pro – Métropole 2023

Annales corrigées de Maths série pro – Métropole 2022

Annales Mathématiques Série pro – Métropole 2024

Annales corrigées de Maths – Métropole 2024



