I. Yemale yu am ñaari deetxam
Bènn yemale bu am ñaari deetxam da fay am melokaan wii $ax+b y+c=0$ $(a$ ; $b$ ak $c$ di ay limum dëgg$)$.
Wutum sottaleek bènn yemale bu jëgoom di 1 ci $\mathbb{R} \times \mathbb{R}$
Doxalin :
Ngir gis ab takk-tànku (couple) limum dëgg buy nekk sottaleek bènn yemale bu jëgoom di 1 ci $\mathbb{R} \times \mathbb{R}$, da ngay jox kènn ci deetxam yi bènn njëkk bu mu manti doon ba noppi ñu daal di gennee keneen ki.
Ab misaal :
Ci $\rm(E_1)$ : $y=-2 x+6$, su fekkee ne $x=0$ konn $y=-2 \times 0+6$ te konn $y=6$
Takk-tànku tomb bii di $(0~ ; 6)$ ab sottali la ci $\rm(E_1)$
Su fekkee ne $x=2$, konn $y = -2 \times 2 +6$ te konn $y = 2$
Takk-tànku limum dëgg bii di $(2 ~; 2)$ ab sottal la ci $\rm(E_1)$.
Mandargaay nataalu sottaleek bènn yemale ci $\mathbb{R} \times \mathbb{R}$
Xam na ñu ne takk-tànku limum dëgg yii di $(0~ ; 6)$ ; $(1~ ; 4)$ ak $(2~ ; 2)$ ay sottalu yemale gii di $(\mathrm E) : 2 x+y=6$ la ñu.
Ci maasale gi nu defal bènn xammalekukaay $\rm (O, I, J)$ na ñu tekk tomb yii di $\rm A(0~ ; 6)$ ; $\rm B(1~ ; 4)$ ak $\rm C(2~ ; 2)$.
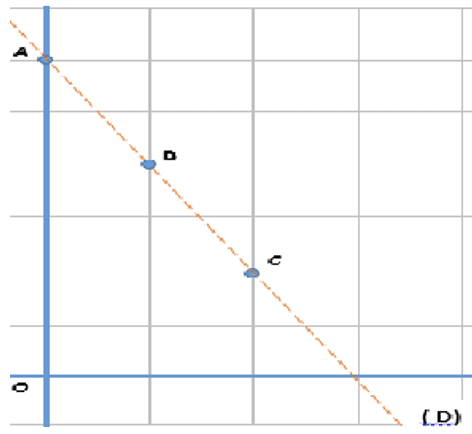
Da ñuy seetlu ne tomb yii di $\rm A(0~ ; 6)$ ; $\rm B(1~ ; 4)$ ak $\rm C(2~ ; 2)$ da ñoo raŋale.
Su bènn rëdd $\rm (D)$ jaaree ci tomb yii di $\rm A, B$ ak $\rm C$, da ñuy naan rëdd wii di $\rm (D)$ te yemaleem di $(\mathrm E): 2 x+y=6$ ab mandargaay nataalu rëdd wii di $\rm (D)$ la.
II. Kureelu ay yemale yu am ñaari deetxam
Ñooy kureel yi am melokaan wii :
$\left\{\begin{array}{l} a x+b y=c \\ a^{\prime} x+b^{\prime} y=c^{\prime} \end{array}\right.$
$a$, $b$, $c$, $a^{\prime}$, $b^{\prime}$ ak $c^{\prime}$ nekk ay limum dëgg.
$x$ ak $y$ ñooy deetxam yi.
Ngir sottali kureel gu mel nònu, man ngaa jëfëndikoo 4 doxalin :
Doxalinu wuutal
Na ñu jël kureel gii :
$$\left\{\begin{array}{l}
3 x-4 y-5=0 \\
2 x+5 y-11=0
\end{array}\right.$$
Ci $\rm (D)$ : $3 x-4 y-5=0$ na ñu binnd $y$ ci anamu $x$ :
$\rm (D_1)$ : $y=\dfrac{3}{4} x-\dfrac{5}{4}$
Ci $\rm(D^{\prime})$ : $2 x+5 y-11=0$, na ñu wuutal $x$ ci binndinam gògu :
$$\begin{array}{l}
2 x+5\left(\dfrac{3}{4} x-\dfrac{5}{4}\right)-11=0 \\
x=3
\end{array}$$
Na ñu raññee njëgum $y$
$$\begin{array}{l}
y=\dfrac{3}{4} x-\dfrac{5}{4}=\dfrac{3}{4} \times 3-\dfrac{5}{4} \\
y=1
\end{array}$$
Da ñuy dëggël ne takk-tànk bii di $(3 ~; 1)$ da fa bokk ci $\rm (D)$ ak $\rm (D')$ konn sottaluk kureel gi mooy takk-tànk bii di $(3 ~; 1)$.
Doxalinu wuutal mooy nga binnd bènn ci deetxam yi ci anamu beneen bi ci bènn ci ñaari yemale yi ba pare nga wuutal ko ci beneen bi ngir am bènn yemale bu jëgoom di 1 te mu am bènn deetxam.
Doxalinu jaxasse wala yokkalante
Na ñu jël kureel gii :
$\left\{\begin{array}{l}
3 x-4 y-5=0 \\
2 x+5 y-11=0
\end{array}\right.$
$\checkmark$ Teggek $x$ :
$\left\{\begin{array}{l}
(3 x-4 y-5=0) \times (2)\\
(2 x+5 y-11=0) \times (-3)
\end{array}\right.$
Ñu daal di am :
$\left\{\begin{array}{l}
6 x-8 y-10=0 \\
-6 x-15 y+33=0
\end{array}\right.$
Bu ñu yokkalante cër si cër, da ñuy am :
$0-23 y+23=0$
$23 y=23$
$y=1$
$\checkmark$ Teggek $y$ :
$\left\{\begin{array}{l}
(3 x-4 y-5=0) \times (5)\\
(2 x+5 y-11=0) \times (4)
\end{array}\right.$
Da ñuy am :
$\left\{\begin{array}{l}
15 x-20 y-25=0 \\
8 x+20 y-44=0
\end{array}\right.$
Bu ñu yokkalante cër si cër, da ñuy am :
$23 x+0-69=0$
$23 x=69$
$x=3$
Da ñuy dëggël ne takk-tànk bii di $(3~ ; 1)$ da fa bokk ci $\rm (D)$ ak $\rm (D')$ konn sottaluk kureel gi mooy $(3~ ; 1)$.
Ngir sottal bènn kureel ci doxalinu jaxasse :
- Da ngay tànn deetxam bi nga bëgga teggi, ci misaal $x$.
- Nga daal di fŭll ñaari cëri bènn ci yemale yi (wala ñoom ñaar su ko laajee) ci ay araf si anam boo xamne deetxam bii di $x$ da fay am ay araf yu feewëloo.
- Nga yokkalante cër si cër ñaari yemale yu bees yi ñu am ci 2. Daal di am bènn yemale bu bees bu jëgoom di 1 te am bènn deetxam donŋ muy $y$.
- Nga sottal yemale bi amoon si 3., daal di gis njëgum y.
- Nga teggi ñaareeli deetxam ci ngay topp poñ yii weesu.
- Nga daal di joxe sottaluk kureel gi.
Doxalinu nataal
Ngir sottal ci anamu nataal kureel gii di : $\left\{\begin{array}{l}x+2 y=3 \\ 2 x-y=1\end{array}\right.$, da ngay nataal rëdd yii di $\rm (D)$ ak $\rm (D')$ te seeniy yemale di $x+2 y=3$ ak $2 x-y=1$.
$\rm (D)$ ak $\rm (D^{\prime})$ da ñuy dogoo ci $\rm A$ mi ay maaskaam di $(1 ~; 1)$.
Konn takk-tànk gii di $(1~ ; 1)$ mooy sottalik kureel gi.
Doxalinu mengale
Da ñuy binnd ñaari yemale ci anamu waññeeku :
$2 x+3 y=4$ da fay joxe $y=\dfrac{-2}{3}x + \dfrac{4}{3}$
$5 x+7=7$ da fay joxe $y=\dfrac{-5}{6} x+\dfrac{7}{6}$
Ñu mengale :
$\begin{array}{l}
-(2 / 3) x+4 / 3=-(5 / 6) x+7 / 6 \\
(5 / 6) x-(2 / 3) x=+7 / 6-4 / 3 \\
(5 / 6) x-(2 / 3) x=+7 / 6-4 / 3 \\
(1 / 6) x=-1 / 6 \\
x=-1
\end{array}$
Su ñu wuutalee ci kènn si yemale bu mu mana doon bu kureel gi, da ñuy am njëgum $y$.
$\begin{array}{l}
y=-(2 / 3)(-1)+4 / 3=2 / 3+4 / 3=2 \\
y=2
\end{array}$
$\color{orangered}{\text{takk-tànku sottal gi mooy } x=-1, y=+2}$
