Yemadi ak kureelu yemadi yu am ñaari deetxam

I. Yemadi yu am ñaari deetxam

Na $a$, $b$ ak $c$ doon ay limum dëgg yoo xamne $(a~ ; b) \neq(0~ ; 0)$.

Melni yemadi yu jëgoom

Dèes na tuddee yemadi bu jëgoom di bènn ci $\mathbb{R} \times \mathbb{R}$ bèpp yemadi bu am bènn ci melokaan yii : $ax+b y+c > 0$ ; $ax+b y+c < 0$ ; $ax+b y+c \geq 0$ wala $ax+b y+c \leq 0$.

Ab takk-tànk $\left(x_1~ ; y_1\right)$ bu ay limum dëgg daa sottal ci kènn si yemadi yi, mungi firi ne $x_1$ ak $y_1$ da ñuy dëggël yemadi gòògu.

$x-y+3<0$ ab yemadi bu jëgoom di bènn la ci $\mathbb{R} \times \mathbb{R}$.

• Ngir $x=1$ ak $y=5$, da ñuy am : $1-5+3=-1$.
  $-1< 0$ dëgg la, konn takk-tànk gii dii $(1 ~; 5)$ ab sottalu yemadi gi la.
• Ngir $x=0$ ak $y=0$, da ñuy am $0-0+3=3$.
  $3 < 0$ du dëgg. Konn $(0~ ; 0)$ du sottalu yemadi gi.

Xaaj maasale

Ci maasale gi ñu wutal bènn xammalekukaay $\rm (O, i, j)$, na ñu jël rëdd wii di $\rm (D)$ te yemaleem di : $ax+by+c=0$.

$\rm (D)$ da fay xaaj maasale gi ci ñaari xaaji maasale :

• Kènn si ñaari xaaji maasale yòyu da fay denc tomb yëpp yi nga xamne seeniy maaskà da ñuy dëggal $a x+b y+c > 0$
• Beneen xaaju maasale gi da fay denc tomb yëpp yi nga xamne seeniy maaskà da ñuy dëggal $a x+b y+c < 0$

Mbooloom sottaleek bènn yemadi da fay daal di nekk konn mbooloom takk-tànkuk maaskaay ay tomb yi nekk ci bènn xaaju maasale.

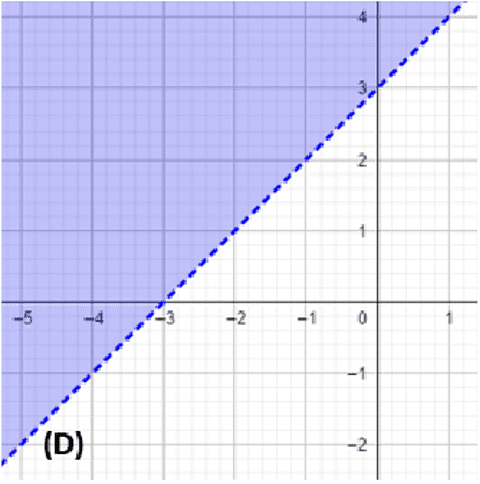
Mbooloom sottaleek yemadi gii di : $x-y+3 < 0$ mooy xaaju maasle, gi peggam di rëdd wii di (D) mi yemaleem di : $x-y+3=0$, te dencul $0(0 ~; 0)$.

II. Kureeli 2 yemadi yu am 2 deetxam

Wonale

$\left\{\begin{array}{l}2 x-y+1<0 \\-x+y-3<0\end{array}\right.$ ab kureelu yemadi yu seeniy jëgoo di bènn la, ci $\mathbb{R} \times \mathbb{R}$ te ay deetxamam di $x$ ak $y$.

Mandargaay nataal

Maasale gi da ñu koo wutal bènn xammalikukaay $\rm (O, i, j)$.

Rëdd yi

$\rm (D)$ mooy rëdd wi yemaleem di : $\rm (D)$ : $2x-y+1=0$
$\rm (D')$ mooy rëdd wi yemaleem di : $\rm(D^{\prime})$ : $-x+y-3=0$

Tomb yi ci rëdd $(\mathrm D) : 2 x-y+1=0$

Su fekkee $x = 0$, konn da ñuy am $2 \times 0 - y+ 1=0$. Konn $y = 1$. Ñu daal di am tomb bii di $\rm A(0~ ; 1)$.

Su fekkee $x=1$, da ñuy am $2\times 1-y +1=0$. Konn $y = 3$. Ñu daal di am tomb bii di $\rm B(1~ ; 3)$.

Tomb yi ci rëdd $(\mathrm D') : - x+y-3 =0$

Su fekkee $x=0$ konn da ñuy am $-0+y-3 =0$. $y = 3$. Ñu daal di am tomb bii di $\rm C(0~ ; 3)$.

Su fekkee $x=1$ konn da ñuy am $1+y-3=0$. Konn $y = 2$. Ñu daal di am tomb bii di $\rm D(-1~ ; 2)$.

Ab seetlu

Goxx bi amul bènn kuloor mooy nataalu mandargaak sottaleek kureel gi.