I. Coordonnées d'un vecteur

Définition

$(\mathrm O, \vec{\imath}, \vec{\jmath})$ un repère du plan.
Soient $\mathrm A\left(x_{\rm A}~ ; y_{\rm A}\right)$ et $\mathrm B\left(x_{\rm B}~ ; y_{\rm B}\right)$ deux points de ce plan.
Le vecteur $\overrightarrow{\rm A B}$ a pour coordonnées $\left(\begin{array}{l}x_{\rm B}-x_{\rm A} \\ y_{\rm B}-y_{\rm  A}\end{array}\right)$.
On note $\overrightarrow{\rm A B}\left(\begin{array}{l}x_{\rm B} - x_{\rm A} \\ y_{\rm B} - y_{\rm  A}\end{array}\right)$.

Propriétés

Soient $\vec{u}\left(\begin{array}{l}x \\ y\end{array}\right)$ et $\vec{v}\left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)$ deux vecteurs.

  • Pour tout réel $k$, le vecteur $k . \vec{u}$ a pour coordonnées $\left(\begin{array}{l}k x \\ k y\end{array}\right)$
  • $\vec{u}=\vec{v}$ si et seulement si $x=x^{\prime}$ et $y=y^{\prime}$.
  • $\vec{u}+\vec{v}$ a pour coordonnées $\left(\begin{array}{l}x+x' \\ y+y'\end{array}\right)$
  • Pour tout vecteur $\vec{u}$ tel que $\vec{u}=x \vec{\imath}+y \vec{\jmath}$ on a : $\vec{u}\left(\begin{array}{l}x \\ y\end{array}\right)$.
  • Pour tout point $\rm M$ du plan, si $\overrightarrow{\rm O M} = x.\vec{\imath} + y.\vec{\jmath}$ alors $\mathrm M(x~ ; y)$.

Vecteurs colinéaires et vecteurs orthogonaux

Le plan est muni d'un repère $\rm (O, \vec i, \vec j)$.
$\overrightarrow{\rm A B}\left(\begin{array}{l}x \\ y\end{array}\right)$ et $\overrightarrow{\rm C D}\left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)$ sont colinéaires équivaut à : $x y^{\prime}-x^{\prime} y=0$
Le plan est muni d'un repère orthonormé $\rm (O, \vec i, \vec j)$.
$\overrightarrow{\rm A B}$ et $\overrightarrow{\rm C D}$ sont deux vecteurs non nuls :
$\overrightarrow{\rm A B}\left(\begin{array}{l}x \\ y\end{array}\right)$ et $\overrightarrow{\rm C D}\left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)$ sont orthogonaux équivaut à : $x x^{\prime}+y y^{\prime}=0$

II. Calcul de la distance entre 2 points

Le plan est muni d'un repère $\rm (O, \vec i, \vec j)$.
$\rm A$ et $\rm B$ sont des points du plan.
Si $\mathrm A\left(x_{\rm A}~ ; y_{\rm A}\right)$ et $\mathrm B\left(x_{\rm B}~ ; y_{\rm B}\right)$ alors $\mathrm{A B} = \sqrt{\left(x_{\rm B} - x_{\rm A}\right)^2 + \left(y_{\rm B} - y_{\rm A}\right)^2}$

Exemple :
Le plan est muni d'un repère $\rm (O, \vec i, \vec j)$.
Soit $\rm A\left(\begin{array}{l}3 \\ 2\end{array}\right)$ et $\rm B\left(\begin{array}{l}2 \\ -2\end{array}\right)$ deux points dans un repère orthonormé $\rm (O, \vec i, \vec j)$.
Calculer la distance $\rm A B$.

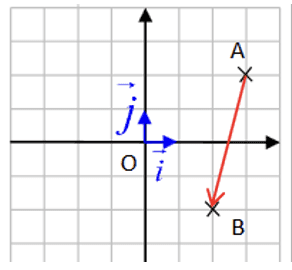
La distance $\rm A B$ est égale à :
$$\begin{aligned}
\rm A B & =\sqrt{(2-3)^2+(-2-2)^2} \\
& =\sqrt{1+16} \\
& =\sqrt{17}
\end{aligned}$$

III. Équations de droite

Définition

Soient $a$, $b$ et $c$ des nombres réels.
Dans le plan muni d'un repère :

  • Toute droite a une équation de la forme $a x+b y+c=0$ où $a$ et $b$ sont des réels tous non nuls.
  • Toute équation de la forme $a x+b y+c=0$, où $a$ et $b$ sont des réels tous non nuls, est une équation de droite.

Dans le plan muni du repère $\rm (O, \vec i, \vec j)$, on donne une droite $\rm (D)$ qui a pour équation $a x+b y+c=0$
On peut transformer cette équation sous la forme $y=a x+b$. avec $a$ et $b$ sont des réels non nuls).

Dans ces conditions :

  • $a$ est le coefficient directeur de la droite $\bf(D)$.
  • $b$ est l'ordonnée à l'origine de la droite $\bf (D)$.

Le plan est muni du repère $\rm (O, \vec i, \vec j)$. La droite $\rm (D)$ passe par les points $\mathrm A\left(x_{\rm A}~ ; y_{\rm A}\right)$ et $\mathrm B\left(x_{\rm A}~ ; y_{\rm B}\right)$
Le coefficient directeur $a$ de $\rm (D)$ est donné par la formule : $a=\dfrac{y_{\rm B}-y_{\rm A}}{x_{\rm B}-x_{\rm A}}$.

Équation de droite passant par 2 points

Dans le plan muni d'un repère $\rm (O~ ; \vec i ~; \vec j)$, on donne les points $\rm A(4~ ;-3)$ et $\rm B(6~ ; 1)$.
Déterminons une équation de la droite $\rm (A B)$.
Considérons un point $\rm M$ du plan tel que $\mathrm M(x~ ; y)$.
On sait que le point $\mathrm{M}$ appartient à $(\mathrm{AB})$ équivaut à $\overrightarrow{\rm A M}$ et $\overrightarrow{\rm A B}$ sont colinéaires.
On a : $\overrightarrow{\rm A M}\left(\begin{array}{l}x-4 \\ y+3\end{array}\right)$ et $\overrightarrow{\rm A B}\left(\begin{array}{l}2 \\ 4\end{array}\right)$.
Le point $\rm M$ appartient à $(A B)$ équivaut à : $4(x-4)-2(y+3)=0$.
$$\begin{array}{r}
4 x-16-2 y-6=0 \\
4 x-2 y-22=0 \\
2 x-y-11=0
\end{array}$$
$2 x-y-11=0$ est une équation de la droite $\rm(AB)$.

Équation de droite passant par un point et parallèle à une droite donnée

Dans le plan muni du repère $\rm (O, \vec i, \vec j)$, on donne les points $\rm A(3~ ; 2)$ ; $\rm B(-1~ ;-4)$ et $\rm C(-2~ ; 1)$.
Déterminons une équation de la droite $\rm (D)$ passant par $\mathrm{C}$ et parallèle à $(\mathrm{AB})$.
Considérons $\rm M$ un point du plan tel que $\mathrm M(x~ ; y)$.
On sait que $\rm M$ appartient à $\rm (D)$ équivaut à $\overrightarrow{\rm C M}$ et $\overrightarrow{\rm A B}$ sont colinéaires.
Or $\overrightarrow{\rm C M}\left(\begin{array}{l}x+2 \\ y-1\end{array}\right)$ et $ \overrightarrow{\rm A B}\left(\begin{array}{c}-4 \\ -6\end{array}\right)$.
Le point $\rm M$ appartient à $\rm (D)$ équivaut à : $-6(x+2)+4(y-1)=0$
$-6 x-12+4 y-4=0$
$-6 x+4 y-16=0$
$-3 x+2 y-8=0$

$-3 x+2 y-8=0$ est une équation de la droite $\rm (D)$.

Équation de droite passant par un point et perpendiculaire à une droite donnée.

Dans le plan muni d'un repère orthonormé $\rm (O, \vec i, \vec j)$, on donne $\rm E(1~ ; 3)$, $\rm F(-2~ ;-6)$ et $\rm G(2~ ;-2)$. Déterminons une équation de la droite $\rm (D)$ passant par $\rm G$ et perpendiculaire à $\rm (E F)$. Considérons un point $\mathrm{M}$ du plan tel que $\mathrm M(x~ ; y)$.
On sait que $\rm M$ appartient à $\rm (D)$ équivaut à $\overrightarrow{\rm G M}$ et $\overrightarrow{\rm E F}$ sont orthogonaux.
Or $\overrightarrow{\rm G M}\left(\begin{array}{l}x-2 \\ y+2\end{array}\right)$ et $\overrightarrow{\rm E F}\left(\begin{array}{l}-2-1 \\ -6-3\end{array}\right), \overrightarrow{\rm E F}\left(\begin{array}{l}-3 \\ -9\end{array}\right)$.
D'où $\rm M$ appartient à $\rm (D)$ équivaut à : $-3(x-2)+(-9)(y+2)=0$
$-3 x+6-9 y-18=0$ 
$-3 x-9 y-12=0$
$x+3 y+4=0$

$x+3 y+4=0$ est une équation de la droite $\rm (D)$.

IV. Positions relatives de 2 droites

Droites parallèles

Le plan est muni du repère $\rm (O, \vec i, \vec j)$.
Les droites $\rm (D)$ et $\rm\left(D^{\prime}\right)$ ont pour coefficients directeurs respectifs $a$ et $a^{\prime}$.
$\rm (D) ~// \left(\rm D^{\prime}\right)$ équivaut à : $a=a^{\prime}$.

Droites perpendiculaires

Le plan est muni du repère orthonormé $\rm (O, \vec i, \vec j)$.
Les droites $\rm (D)$ et $\rm\left(D^{\prime}\right)$ ont pour coefficients directeurs respectifs $a$ et $a^{\prime}$.
$\rm\left.(D) \perp D^{\prime}\right)$ équivaut à : $a \times a^{\prime}=-1$.