I. Cas du triangle

Configurations de Thalès

Deux triangles forment une configuration de Thalès s'ils sont déterminés par deux droites sécantes qui elles à leur tour sont coupées par deux droites parallèles.

Ces trois figures sont dites configurations de Thalès.

Théorème direct

$\mathrm{ABC}$ est un triangle.
$\rm M$ est un point de droite $(\mathrm{AB})$ et $\mathrm{N}$ un point de la droite $(\mathrm{AC})$.
Si $(\mathrm{MN}) / /(\mathrm{BC})$ alors $\rm\dfrac{A M}{A B}=\rm\dfrac{A N}{A C}$.

Remarque :

On peut utiliser la propriété de Thalès pour calculer des distances ou justifier une égalité de quotients.

Conséquence

$\rm A B C$ est un triangle,
$\rm M \in(A B)$ et $\rm N \in(A C)$ :
Si $\rm (M N) ~//~(B C)$ alors $\rm\dfrac{A M}{A B}=\dfrac{A N}{A C}=\dfrac{M N}{B C}$

Remarque :

La propriété de Thalès et la conséquence permettent de calculer la mesure des segments.

Réciproque

$\rm A B C$ est un triangle.
$\rm M$ est un point de la droite $\rm (A B)$ ; $\rm N$ est un point de la droite $\rm (A C)$ tel que la position de $\rm M$ par rapport à $\rm A$ et $\rm B$ soit la même que celle de $\rm N$ par rapport à $\rm A$ et $\rm C$.

Si $\rm\dfrac{A M}{A B}=\dfrac{A N}{A C}$ alors $\rm (M N)~ // ~(B C)$

Remarque :

La reciproque de la proprieté de Thalès permet de justifier le parallélisme des droites.

Partage dun segment en des segments de même longueur

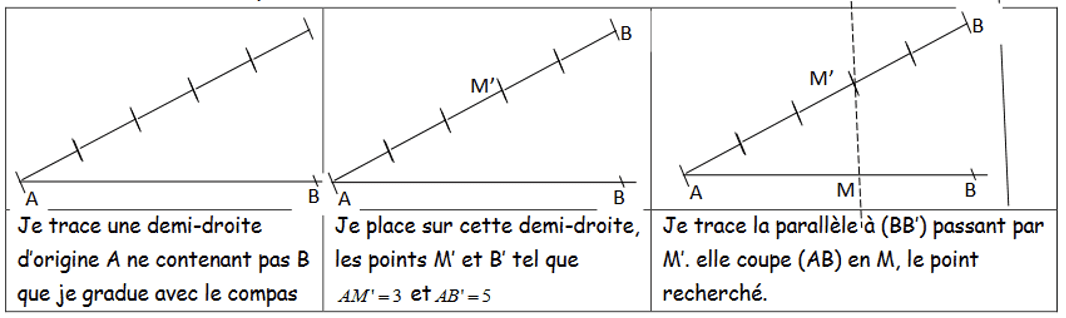
Méthode :

Pour placer sur le segment $\rm [A B]$, le point $\rm M$ tel que $\mathrm{A M}=\dfrac{a}{b}$ : $a$ et $b$ étant deux entiers naturels non nuls donnés, on peut procéder comme suit (cas où $a=3$ et $b=5)$.