I. Addition vectorielle
A, B et C sont trois points du plan. On appelle somme des vecteurs →AB et →BC, le vecteur →AC.
On note : →AB+→BC=→AC.
Cette égalité est appelée égalité de Chasles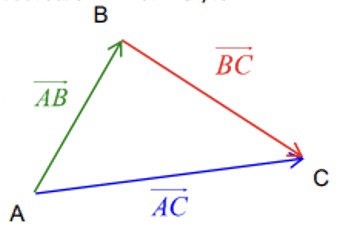
Vecteurs opposés
A, B et C sont trois points du plan.
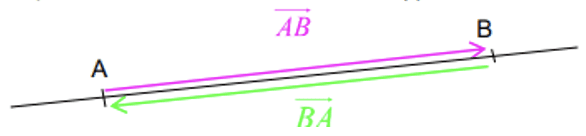
On a : →AB+→BA=→AA=→0
On dit que →AB et →BA sont des vecteurs opposés. On note →BA=−→AB
II. Multiplication d'un vecteur par un nombre
Définition
On appelle produit du vecteur non nul →AB par le nombre réel non nul k, le vecteur →MN.
- (AB) // (MN) ont la même direction ;
- →AB et →MN :
- ont le même sens si k>0 ;
- ont des sens contraires si k<0
- MN=|k|AB.
Remarque :
- Le produit du vecteur nul par un nombre réel est le vecteur nul ;
- Le produit du vecteur →AB par 0 est le vecteur nul →0 ;
- Le produit du vecteur →AB par un nombre k non nul est noté : k→AB.
Exemples :

Les vecteurs →AB, 1.5→AB ont la même direction.
→AB et 1,5→AB sont de même sens.
→AB et −3→AB sont de sens contraire.
Propriétés
A, B, C et D sont des points du plan. k et h sont des nombres réels. On a :
- k(h→AB)=(kh)→AB.
- k→AB+k→CD=k(→AB+→CD).
- k→AB+h→AB=(k+h)→AB.
- 1→AB=→AB.
III. Vecteurs de même direction et vecteurs colinéaires
Vecteurs de même direction
Propriété
A, B, C et D sont quatre points du plan.
Les vecteurs →AB et →CD ont la même direction signifie qu'on peut trouver un nombre réel k non nul tel que : →AB=k→CD
Vecteurs colinéaires
Définition
On dit que des vecteurs sont colinéaires lorsqu'ils ont la même direction, ou lorsque l'un d'eux est le vecteur nul.
Exemple :
→AB=3→CD équivaut à →AB et →CD ont même direction alors →AB et →CD sont colinéaires.
Propriété
A et B sont deux points du plan.
Un point M appartient à la droite (AB) équivaut à →AM et →AB sont colinéaires.
Conséquences
Vecteur et milieu
Si le point I est le milieu de [AB], alors →AB=2→AI
![]()
Si
Alors est le milieu de .
Points alignés
Si , et sont alignés
Alors
![]()
Si
Alors , et sont alignés
Droites parallèles
Si alors

Si alors et sont parallèles.



