I. Théorème 1
Si une droite passe par les milieux de deux côtés d'un triangle alors elle est parallèle au support du troisième côté.
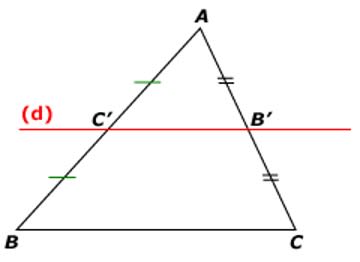
C′ milieu de [AB] et B′ milieu de [AC] donc (d) est parallèle à (BC).
II. Théorème 2
Si un segment joint les milieux de deux côtés d'un triangle alors il a pour longueur la moitié de la longueur du troisième côté.
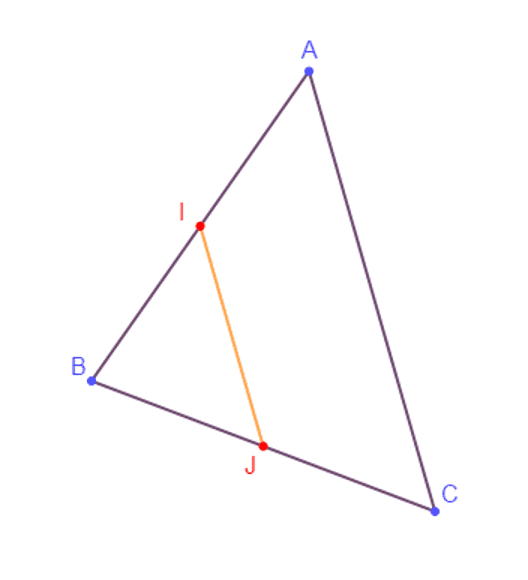
I milieu de [AB] et J milieu de [BC] donc IJ=12AC
III. Théorème 3
Si dans un triangle, une droite passe par le milieu d'un côté et est parallèle à un autre côté alors elle passe par le milieu du troisième côté.
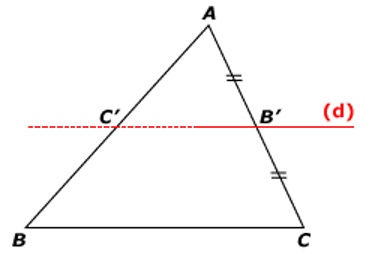
B′ milieu de [AC] et (d) parallèle à (BC) donc C′ milieu de [AB].
IV. Théorème 4
Si trois droites parallèles découpent sur une sécante deux segments consécutifs de même longueur alors elles découpent sur toute autre sécante deux segments consécutifs de même longueur.



