Définition
La projection orthogonale d'un point $\mathrm{M}$ sur une droite $(d)$ est le point $\mathrm{H}$ d'intersection de la droite $(d)$ et de la perpendiculaire à $(d)$ passant par $\rm M$.
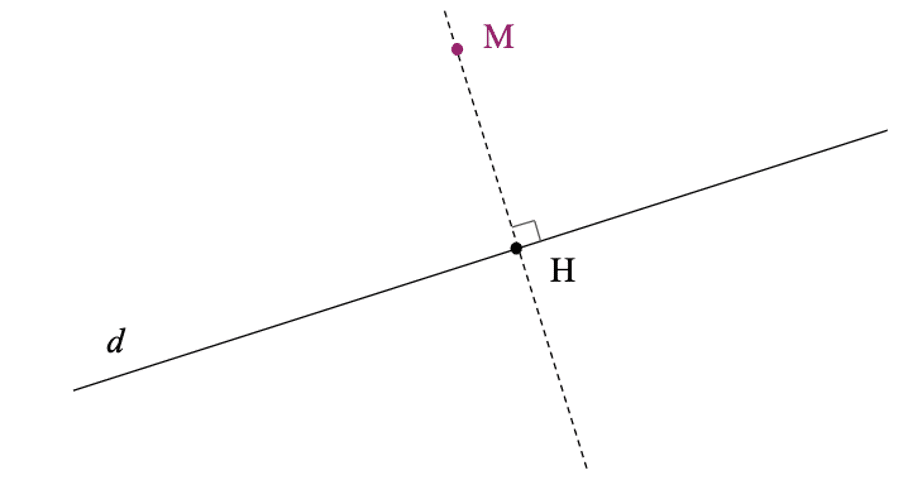
$\rm H$ est le projeté orthogonal du point $\mathrm{M}$ sur la droite $(d)$.
Propriétés
- Le projeté d'un segment est un segment qui peut être réduit à un point.
- Le milieu d'un segment se projette au milieu du segment image.
Repérage dans le plan
- Coordonnées du milieu d'un segment
Soient $\mathrm{A}\left(x_{\mathrm{A}} ~; y_{\mathrm{A}}\right) ; \mathrm{B}\left(x_{\mathrm{B}} ~; y_{\mathrm{B}}\right)$ et $\mathrm{M}\left(x_{\mathrm{M}} ~; y_{\mathrm{M}}\right)$
Si $\rm M$ est le milieu du segment $\rm [AB]$ alors :
$x_{\mathrm{M}}=\dfrac{x_{\mathrm{A}}+x_{\mathrm{B}}}{2}$ et $y_{\mathrm{M}}=\dfrac{y_{\mathrm{A}}+y_{\mathrm{B}}}{2}$ - Carré de la distance entre $\bf 2$ points
Soient $\mathrm{A}\left(x_{\mathrm{A}}~ ; y_{\mathrm{A}}\right)$ et $\mathrm{B}\left(x_{\mathrm{B}} ~; y_{\mathrm{B}}\right)$ alors :
$\mathrm{AB}^2=\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^2+\left(x_{\mathrm{B}}-y_{\mathrm{A}}\right)^2$
