Statistiques

I. Vocabulaire

• La population est un ensemble faisant l'objet d'une étude statistique.
• Un élément de la population est un individu ou une unité statistique.
• On observe des caractères qui prennent différentes valeurs.
• Un caractère est quantitatif si ses valeurs s'expriment par un nombre sinon il est qualitatif. Un caractère prend une valeur donnée.
• L'effectif total est le nombre d'individus de la population. Il est noté $\rm N$.
• La fréquence d'une valeur du caractère est le rapport : $\dfrac{n_i}{\rm N}$.
• Le mode est la modalité qui a le plus grand effectif. Une série statistique peut avoir plusieurs modes.
• La moyenne est un nombre qui caractérise une « position » des valeurs du caractère d'une série statistique à caractère quantitatif.

On note $x_1$, $x_2$, $\ldots$, $x_p$ les différentes valeurs prises par un caractère quantitatif ; $n_1$, $n_2$, $\ldots$, $n_p$ les effectifs respectifs de ces valeurs et $\mathrm{N}$ l'effectif total.
La moyenne $x=\dfrac{x_1 \times n_1+x_2 \times n_2+\ldots + x_p \times n_{p}}{\rm N}$

II. Représentations graphiques

Diagramme en bâtons

Dans un repère d'axes perpendiculaires, on marque en abscisses les modalités et en ordonnées les effectifs.
Chaque modalité est représentée par un segment dont la longueur est proportionnelle à l'effectif.

Voici le diagramme en bâtons représentant une série de notes obtenues par une classe à un contrôle.

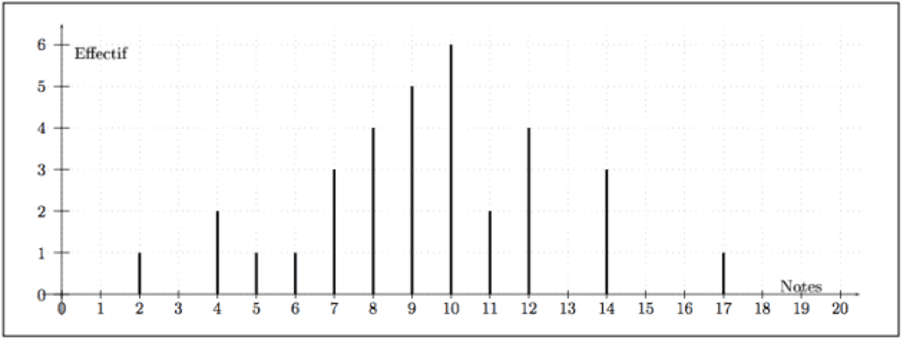
Diagramme à bandes 

Dans un repère d’axes perpendiculaires, on marque en abscisse les modalités et en ordonnées les effectifs. Chaque modalité est représentée par un rectangle dont la longueur est proportionnelle à l'effectif. Tous les rectangles ont la même largeur.

Diagramme en barres

Définition

Un diagramme en barres (ou en bâtons) permet de visualiser rapidement des données et de les comparer. Les hauteurs sont proportionnelles aux effectifs (ou aux fréquences) de chaque valeur de la série.

Exemple :

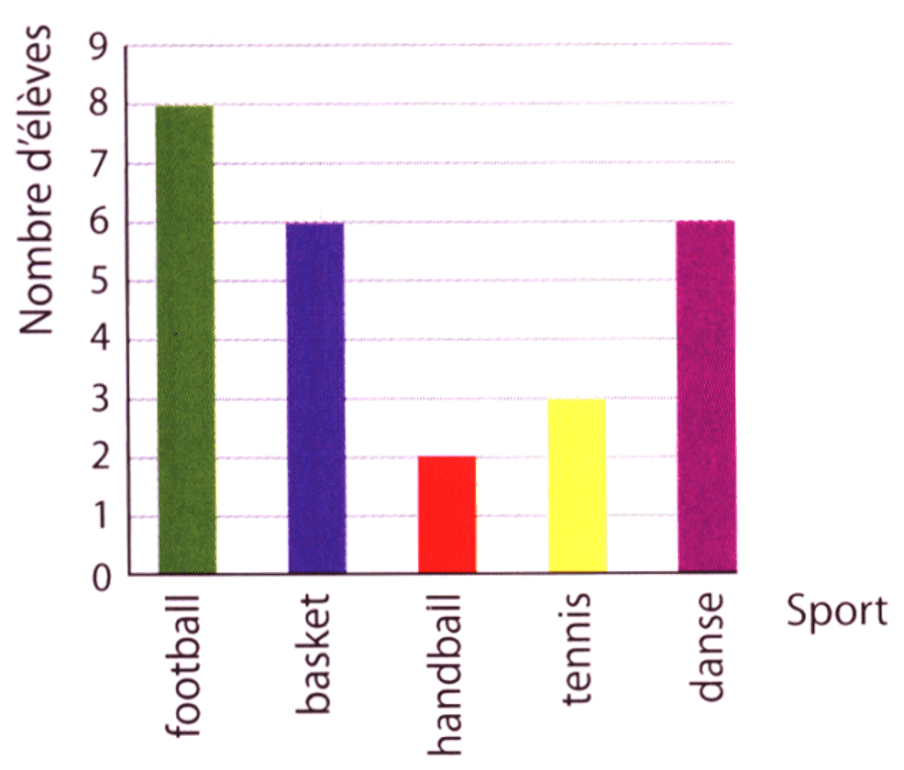
Diagramme circulaire

On trace un cercle qu'on partage en différents secteurs. Chaque modalité est représentée par un secteur d’aire proportionnelle à l'effectif de la modalité.

Pour chaque modalité, l'angle au centre du secteur correspond à la mesure :

$\dfrac{360° \times \text{effectif de la modalité}}{\text{effectif total}}$

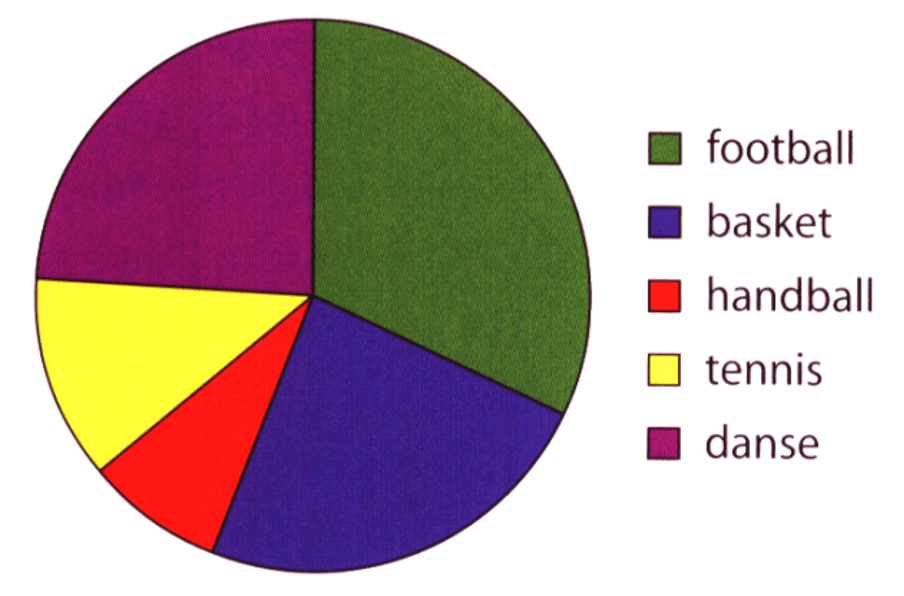
Diagramme semi-circulaire

On le construit comme le diagramme circulaire mais en remplaçant le cercle par un demi-cercle.
Pour chaque modalité, l'angle au centre du secteur correspond à la mesure :
$\dfrac{180° \times \text {effectif de la modalité }}{\text { effectif total }}$