Translation

On considère trois points du plan $\rm A$, $\rm B$ et $\rm C$.

La translation définie par les points $\rm A$ et $\rm B$ (dans cet ordre) transforme le point $\rm C$ en un point $\rm D$ du plan tel que le quadrilatère $\rm ABDC$ est un parallélogramme.

On dit que le point $\rm D$ est l’image du point $\rm C$ par la translation définie par les points $\rm A$ et $\rm B$.

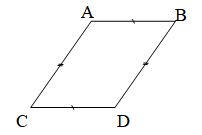
Une translation définie par les points $\rm A$ et $\rm B$ est déterminée par :

• Un axe : la droite $\rm (AB)$ ;
• Un sens : du point $\rm A$ vers le point $\rm B$ ;
• Une longueur : la longueur $\rm AB$.

Propriétés

Une translation :

• conserve les distances : un segment et son translaté ont même longueur ;
• conserve l’alignement : le translaté d’une droite est une droite ;
• conserve les angles : un angle et son translaté ont même mesure ;
• conserve les aires : une figure et son translaté ont la même aire.