Translations et vecteurs

I. Translations

Définition

Soit $3$ points $\rm A$, $\rm B$ et $\rm P$ distincts et $t$ la translation qui transforme le point $\rm A$ en $\rm B$.

• Lorsque le point $\rm P$ n'appartient pas à la droite $\rm (AB)$, l'image du point $\rm P$ par la translation $t$ est le point $\rm P'$ tel que $\rm ABP'P$ est un parallélogramme.
• Lorsque le point $\rm P$ appartient à la droite $\rm (A B)$, l'image du point $\rm P$ par la translation $t$ est le point $\mathrm{P}^{\prime}$ tel que les segments $\left[\mathrm{AP}^{\prime}\right]$ et $[\mathrm{BP}]$ ont le même milieu.

Propriétés

La translation possède plusieurs propriétés importantes concernant la transformation des figures géométriques.

• Dans une translation, l'image d'un segment est un segment qui lui est parallèle et de même longueur.
• Dans une translation, l'image d'une droite est une droite qui lui est parallèle.
• Dans une translation, l'image d'une demi-droite est une demi-droite parallèle et de même sens.
• Dans une translation, l'image d'un cercle est un cercle de même rayon ; son centre est l'image du centre.

La translation conserve l'alignement, les longueurs, les angles, les aires, le parallélisme et l'orthogonalité.

II. Vecteurs

Caractérisation d'un vecteur

Le vecteur $\rm\overrightarrow{AB}$ est caractérisé par trois éléments fondamentaux.

• Sa direction qui est celle de la droite $\rm (AB)$.
• Son sens qui est celui de la demi-droite $\rm AB$.
• Sa longueur qui est celle du segment $\rm [AB]$.

Il est représenté par une flèche.

Vecteurs égaux et vecteurs opposés

Les relations entre vecteurs se définissent selon leurs caractéristiques.

• $2$ vecteurs sont égaux s'ils ont la même direction, le même sens et la même longueur.
  
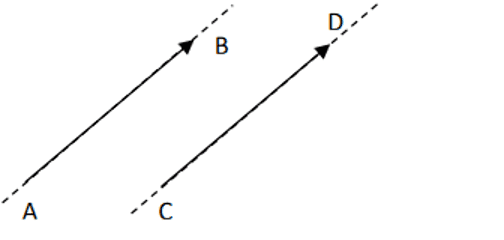
  $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{CD}}$
  
  
• $2$ vecteurs sont opposés s'ils ont la même direction, la même longueur mais des sens contraires.
  
  
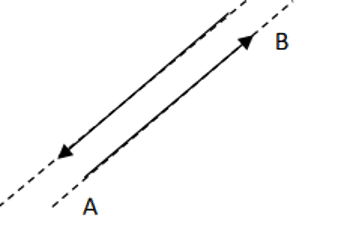
  $\overrightarrow{\mathrm{AB}}$ et $\overrightarrow{\mathrm{BA}}$ sont opposés.

Vecteur et parallélogramme

Il existe une relation fondamentale entre les vecteurs et les parallélogrammes.

• Si $\rm A B C D$ est un parallélogramme alors $\rm\overrightarrow{A B}=\overrightarrow{C D}$.
• Si $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}}$ et les points $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$ et $\mathrm{D}$ ne sont pas alignés alors le quadrilatère $\rm A B C D$ est un parallélogramme.

Milieu d'un segment et vecteur

Le concept de milieu peut être exprimé à l'aide des vecteurs.

• Si un point $\rm I$ est le milieu d'un segment $[\mathrm{AB}]$ alors $\overrightarrow{\mathrm{AI}} = \overrightarrow{\mathrm{IB}}$.
• Si $3$ points $\rm A$, $\rm I$, $\rm B$ sont tels que $\rm \overrightarrow{A I}=\overrightarrow{I B}$ alors $\rm I$ est le milieu de $\rm [A B]$.