I. Prisme droit

Un prisme droit est un solide dont les faces latérales sont des rectangles et les bases polygones superposables.

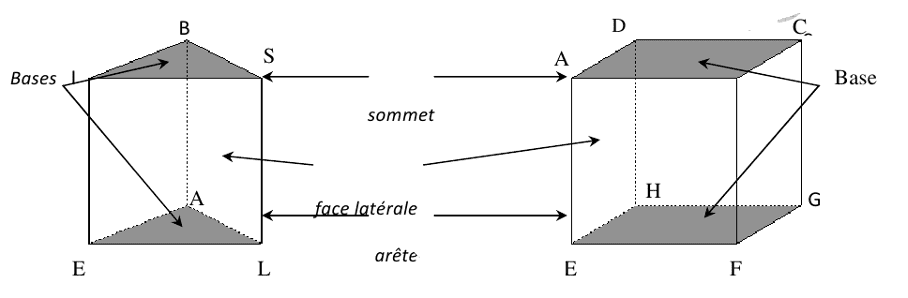
L’ensemble des faces latérales forme la surface latérale.

Une hauteur d’un prisme droit est une arête perpendiculaire aux bases (exemple : $\rm [AB]$, $\rm [SL]$, …).

Autrement dit, la hauteur est la longueur de l’une de ces arêtes.

Un pavé droit est un prisme droit particulier dont les bases sont des rectangles.

Le cube est un prisme droit dont toutes les faces sont des carrés superposables.

Pour représenter le patron d’un prisme droit, il faut :

Construire une des bases, qui est un triangle ou un rectangle, puis on trace une face latérale qui est un rectangle dont les côtés sont un côté de la base et la hauteur du prisme droit.
Tracer la seconde base, qui est symétrique au premier par rapport à l'un des axes de symétrie du rectangle.
Compléter le patron en traçant les deux dernières faces latérales du prisme droit, qui sont des rectangles.

II. Parallélisme et orthogonalité dans l’espace

Deux droites de l’espace sont parallèles si elles sont coplanaires (appartiennent à un seul plan) et sans point commun.
Deux plans sont parallèles s’ils sont confondus ou sans point commun.
Une droite et un plan sont parallèles lorsqu’ils n’ont aucun point commun.

Deux droites de l’espace sont orthogonales lorsque leurs parallèles passant par un point quelconque de l’espace sont perpendiculaires.
Dire qu’une droite est orthogonale à un plan, signifie que cette droite est orthogonale à toutes les droites de ce plan.
Deux plans $\rm P$ et $\rm P’$ de l’espace sont orthogonaux, si toute droite $\rm (D)$ de $\rm P$ est orthogonale à toute $\rm (D’)$ de $\rm P’$.

On parle de droites perpendiculaires, lorsqu’elles sont coplanaires.

Deux droites de même plan et perpendiculaires sont orthogonales, mais deux droites orthogonales ne sont pas nécessairement dans un même plan.

L’aire latérale d’un prisme droit est la somme des aires de ses faces latérales.
L’aire latérale d’un prisme droit est aussi égale au périmètre de base multiplié par sa hauteur.
L’aire totale d’un prisme droit est la somme de son aire latérale et des aires de ses bases.

Le volume d’un prisme droit est égal à son aire de base multiplié par sa hauteur.
Autrement dit, si $\rm B$ est l’aire d’une base, $h$ la hauteur et $\rm V$ son volume, alors $\mathrm{V = B} \times h$.