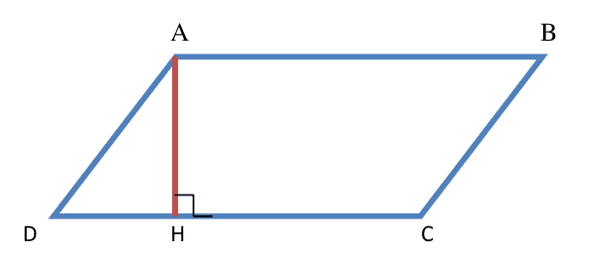
Xamale
Ab wet-yu-làŋ mooy bènn ñeentikoñ boo xamne wetam yi feewëloo da ñoo wet-làŋ

Ay jagle
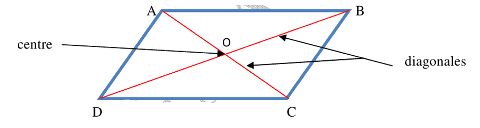
1) Ci bènn wet-yu-làŋ, galaŋ yi da ñuy dogoo ci seen digg.
Tomb bòbu da fay nekk diggu safaanook jàkkaarle bu wet-yu-làŋ bi.
2) Ci bènn wet-yu-làŋ, wet yi feewëloo da ñuy yemoo guddaay.
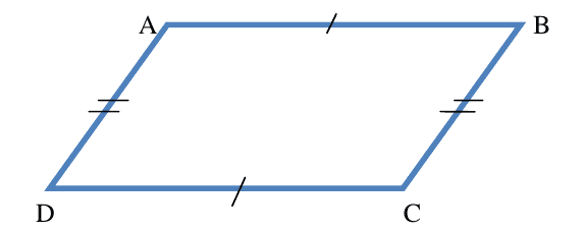
ABCD ab wet-yu-làŋ la, kon AB=DC te AD=BC.
3) Ci bènn wet-yu-làŋ, ñaari angal yu feewëloo da ñuy yem natt.
Ci bènn wet-yu-làŋ, ñaari angal yu toftalante da ñuy ëppalante.

ABCD ab wet-yu-làŋ la, kon ˆA=ˆC te ˆB=ˆD :
- ˆA+ˆB=180∘ ;
ˆB+ˆC=180∘ ;
ˆC+ˆD=180∘ ;
ˆD+ˆA=180∘.
Xammeekuk bènn wet-yu-làŋ
1) Su wet yi feewëloo ci bènn ñeentikoñ yëpp da ñoo wet-làŋ, kon ñeentikoñ bi ab wet-yu-làŋ la.

(AB)//(DC) et (AD)//(BC), kon ABCD ab wet-yu-làŋ la.
2) Su galaŋu bènn ñeentikoñ dogoo ci seen digg, kon ab wet-yu-làŋ la.
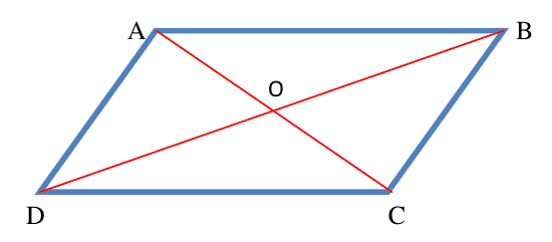
O mooy digguk [AC] te O mooy digguk [BD], kon ABCD ab wet-yu-làŋ la.
3) Su bènn ñettkoñ amee ay angal yu feewëloo yu yem natt ñaar ñaar, kon ab wet-yu-làŋ la.
4) Su fekke ne ci bènn ñeentikoñ, ñaari dendaleek angal yu toftalante yu nekk da ñoo dolliwante, ñeentikoñ bòbu ab wet-yu-làŋ la.
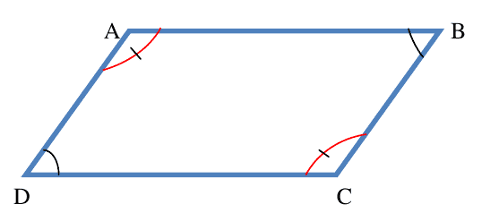
ˆA=ˆC te ˆB=ˆD, kon ABCD ab wet-yu-làŋ la.
- ˆA+ˆB=180∘ ;
- ˆB+ˆC=180∘ ;
- ˆC+ˆD=180∘ ;
- ˆD+ˆA=180∘.
Yaatuwaayuk bènn wet-yu-làŋ
Su ABCD doonee bènn wet-yu-làŋ, kon Yaatuwaay(ABCD) =sukkëndikukaay×kawewaay= DC×AH.