Le symétrique d'un point $\rm A$ par la symétrie de centre $\mathrm{O}$ est le point $\rm A'$ tel que le point $\mathrm{O}$ est le milieu du segment $\rm [AA]'$.
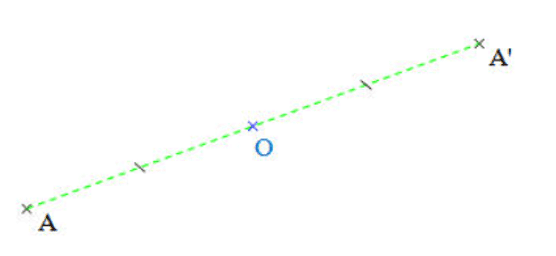
Centre de symétrie
Si une figure est son propre symétrique par la symétrie de centre $\rm O$, on dit que le point $\mathrm{O}$ est centre de symétrie de la figure.
Symétrique d'une figure simple - figures symétriques
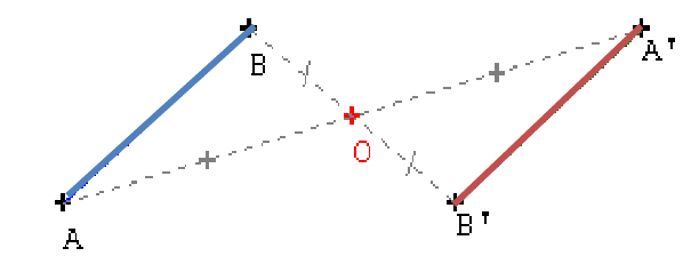
Par une symétrie centrale, l'image d'une droite est une droite, l'image d'une demi-droite est une demi-droite, l'image d'un segment est un segment.
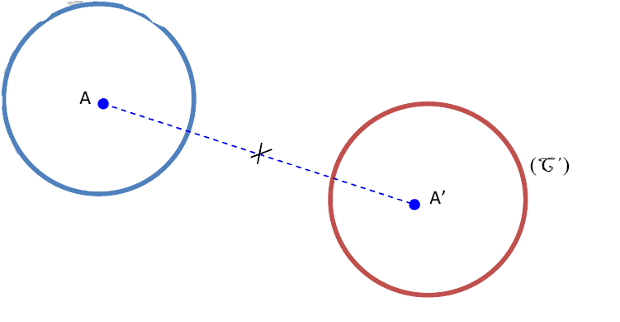
Le symétrique du cercle du cercle $\rm (C)$ par rapport au point $\rm O$ est le cercle $\rm (C’)$.
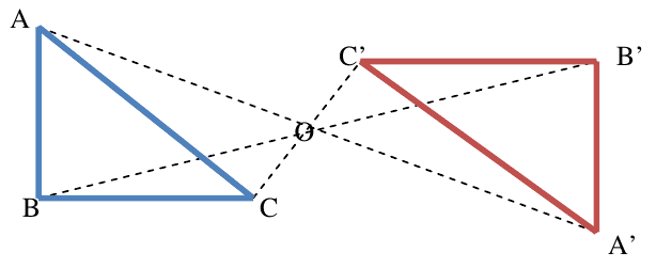
Le symétrique du triangle $\rm ABC$ par rapport au point $\rm O$ est le triangle $\rm A’B’C’$.
Par une symétrie centrale, l’image d’un angle est un angle.
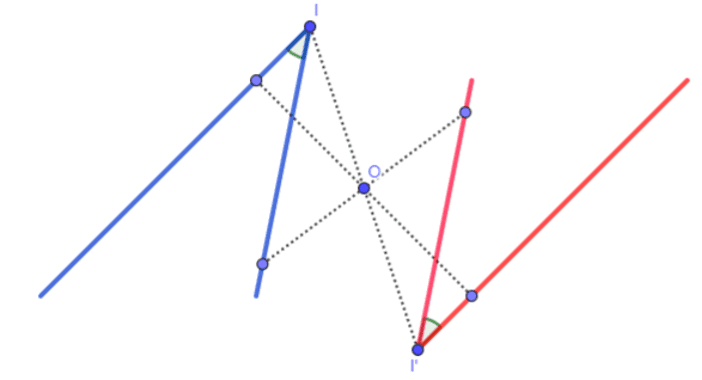
Par une symétrie centrale, l’image d’un rectangle est un rectangle.
Par une symétrie centrale, l’image d’un carré est un carré.
Propriétés de la symétrie centrale
La symétrie centrale :
- conserve les distances : par une symétrie centrale, l’image d’un segment est un segment parallèle de même longueur.
- conserve l’alignement : lorsque des points sont alignés alors leurs symétriques sont alignés.
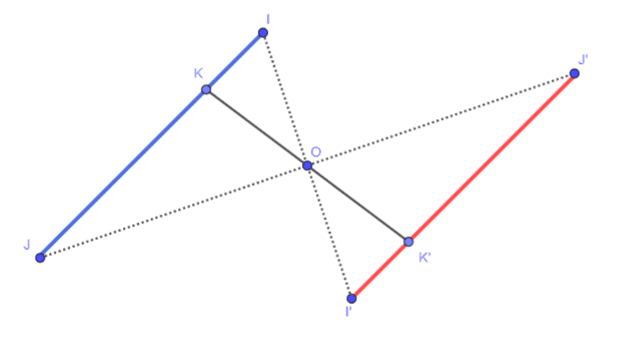
- conserve les angles : un angle et son symétrique ont même mesure ;
- conserve les aires : une figure et son symétrique ont la même aire.
