I. Les différents angles

Deux demi-droites définissent deux parties du plan $\rm \widehat{BAC}$ et $\rm \stackrel{\lor}{BAC}$. Chaque partie est un angle. Le point $\rm A$ est le sommet de l'angle rose $\rm \widehat{B A C}$. Les demi-droites $\rm [AB)$ et $\rm [A C)$, d'origine commune $\rm O$, sont les côtés de l'angle rose.

Angles particuliers

• Angle droit : Si les supports des demi-droites $\rm [A B)$ et $\rm [A C)$ sont perpendiculaires, alors l'angle $\rm \widehat{B A C}$ est un angle droit.
• Angle plat : Si les demi-droites $[\mathrm{AB})$ et $[\mathrm{AC})$ sont opposées, alors l'angle $\rm \widehat{B A C}$ est un angle plat.
• Angle nul : Si les demi-droites $[\mathrm{AB})$ et $(\mathrm{AC})$ sont confondues, alors l'angle $\rm \widehat{B A C}$ est un angle nul.

Angles adjacents

Définition : Deux angles ayant un sommet commun, un côté commun, et sont situés de part et d'autre de ce côté commun sont dits adjacents.
L'instrument qui permet de mesurer les angles s'appelle un rapporteur. Le rapporteur est un demi-cercle gradué en général de $0$ à $180°$.
Le centre du demi-cercle est appelé centre du rapporteur. La ligne passant par $\rm O$ et la graduation $0°$ est la « ligne du zéro ».

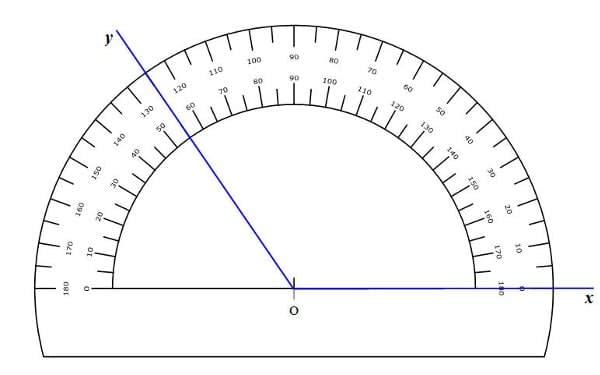
• L'unité de mesure d'angle est le degré noté $°$.
• La mesure d'un angle peut aussi s'exprimer en grade noté $\rm gr$.
  • Un angle droit mesure $90°$ ou $\bf\color{red}{100~gr}$.
  • Un angle plat mesure $180°$ ou $\bf\color{red}{200 ~gr}$.

II. Mesurer un angle

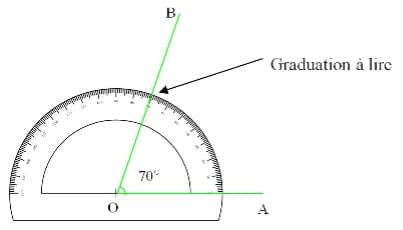
Pour mesurer l'angle $\rm\widehat{AOB}$, on utilise un rapporteur :

• On place le centre du rapporteur sur le point $\rm O$.
• On place la graduation $0$ sur la demi-droite $\rm [OA)$ (en la prolongeant si nécessaire).
• On lit sur le rapporteur à quelle graduation la demi-droite $\rm [OB)$ (en la prolongeant si nécessaire) coupe le demi-cercle extérieur du rapporteur.

Ici, on obtient : $\rm\widehat{AOB}=70°$

• Un angle aigu est un angle plus petit qu'un angle droit. Sa mesure est comprise entre $0°$ et $90°$.
• Un angle obtus est un angle plus grand qu'un angle droit. Sa mesure est comprise entre $90°$ et $180°$.

Deux angles sont complémentaires lorsque leur somme est $90°$.
Deux angles sont supplémentaires lorsque leur somme est $180°$.

• La bissectrice d'un angle est la droite qui passe par le sommet de cet angle et qui le partage en 2 angles de même mesure.
• Le symétrique d'un angle par rapport à une droite donnée est un angle de même mesure (superposable au premier).