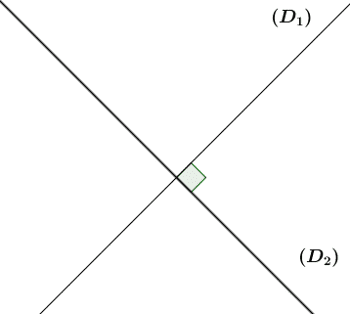
Deux droites sécantes qui forment un angle droit sont appelées des droites perpendiculaires.
- On peut tracer autant de droites que l’on veut perpendiculaires à une droite donnée.
- Par un point, on ne peut tracer qu’une seule droite perpendiculaire à une droite donnée.
- Pour tracer deux droites perpendiculaires, on trace d’abord une droite. On marque un point sur la droite et on place l’équerre sur la droite de manière à ce que l’angle droit parte de ce point. On trace la seconde droite le long de l’équerre, puis on prolonge cette deuxième droite avec la règle.
I. Médiatrice d’un segment
La médiatrice d’un segment est la droite qui coupe perpendiculairement le segment en son milieu.
Elle est constituée de l’ensemble des points équidistants des extrémités du segment.
Deux droites qui ne sont pas sécantes sont appelées des droites parallèles.
Exemple :
Pour exprimer qu’une droite est parallèle à une autre, on utilise le symbole « // ».
Deux droites parallèles ont toujours le même écartement, elles ne se coupent jamais, même si on les prolonge.

Pour vérifier que deux droites sont parallèles, on place la règle et l’équerre de manière perpendiculaire, et on mesure l’écartement des deux droites à deux points différents. Si elles sont parallèles, tous les segments perpendiculaires qui les relient ont la même longueur.
Pour tracer deux droites parallèles, on trace une droite (a) et deux perpendiculaires. Avec la règle, on mesure deux fois le même écartement et on les signale par deux points. On relie ces points pour former la droite parallèle à la droite (a).
II. Théorèmes des droites parallèles et perpendiculaires
Si deux droites sont parallèles, toute droite parallèle à l’une est parallèle à l’autre.
Si deux droites sont parallèles, toute droite perpendiculaire à l’une est perpendiculaire à l’autre.
Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entre elles.



