I. Parallélépipède rectangle
Un parallélépipède rectangle ou pavé droit est un solide ayant six faces rectangles superposables deux à deux ; huit sommets et douze arêtes.
En ouvrant un pavé droit, on obtient son développement ou son patron.
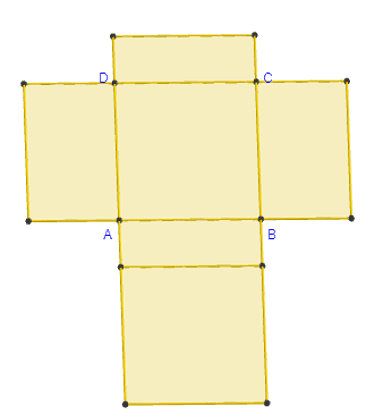
Le cube est un pavé droit dont les faces sont des carrés.
La droite $\rm (AE)$ est perpendiculaire à la fois à $\rm (EH)$ et $\rm (EF)$. La droite $\rm (HG)$ est contenue dans un même plan que $\rm (EH)$ et $\rm (EF)$. On dit que les droites $\rm (AE)$ et $\rm (HG)$ sont orthogonales.
Deux droites perpendiculaires (comme $\rm (AE)$ et $\rm (EH)$) sont également orthogonales.
Deux droites orthogonales ne sont pas toujours perpendiculaires.
Si les arêtes d’un pavé droit mesurent respectivement $a$, $b$ et $c$ comme l’indique la figure :
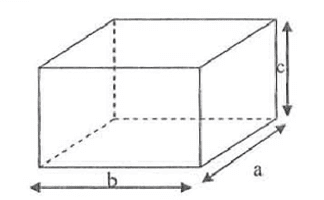
Alors le volume $\rm V$ de ce pavé droit s’écrit :
$\mathrm V = a \times b \times c = \text{aire d’une base} \times \text{hauteur}$.
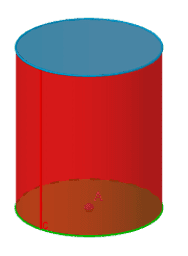
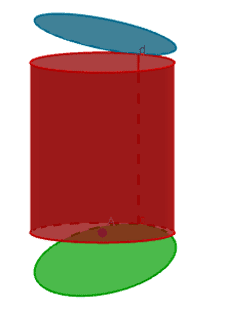
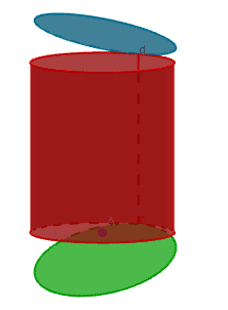
II. Cylindre droit
Un cylindre est un solide dont les deux bases sont des disques.
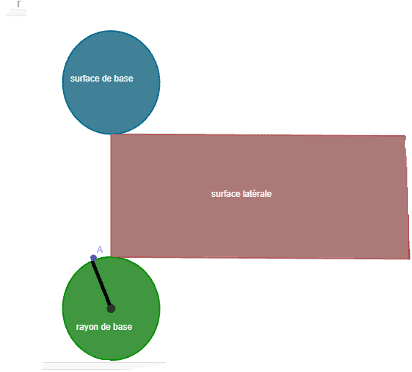
En ouvrant un cylindre par les deux bases et par la hauteur, on obtient son développement ou son patron.
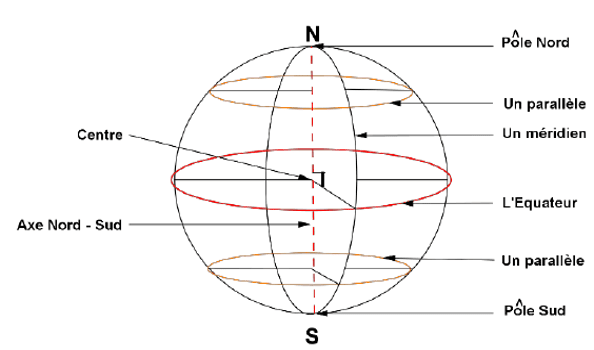
III. Sphère et boule
Une sphère est une surface continue constituée de tous les points situés à une même distance appelé centre de la sphère.
La valeur $\rm R$ de cette distance au centre est appelée rayon de la sphère.
Soit $\rm I$ le centre de la sphère et $\rm S$ un de ses points alors $\rm IS$ est un rayon.
Boule : l’ensemble des points de l’espace dont la distance au point I est inférieure ou égale au rayon est la boule de centre I et de rayon $\rm R$.
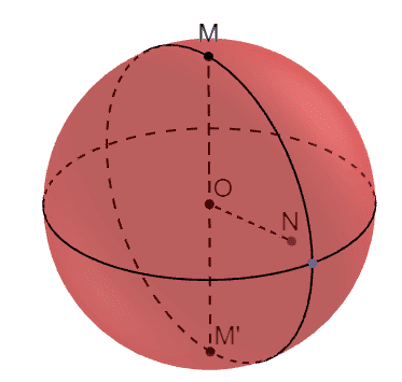
Tout cercle de centre $\rm O$ et de rayon $\rm R$ est un grand cercle de la sphère.
IV. Formules de calcul d’aires et de volumes
| Pavé droit de longueur $\rm I$ et de hauteur $\rm h$ | Cylindre droit de base $\rm R$ et de hauteur $\rm h$ | Sphère de rayon $\rm R$ | Boule de rayon $\rm R$ | |
| Aire de base | $\color{orange}{\rm L\times I}$ | $\color{orange}{\pi\rm R^2}$ | ||
| Aire latérale | $\color{orange}{\rm 2(L+I) \times h}$ | $\color{orange}{\rm 2\pi Rh}$ | ||
| Aire totale | Aire de base + Aire latérale | Aire de base + Aire latérale | $\color{orange}{\rm 4\pi R^2}$ | |
| Volume | $\color{orange}{\rm L \times l \times h}$ | $\color{orange}{\rm \pi R^2h}$ | $\color{orange}{\rm \dfrac{4}{3}\pi R^2}$ |
