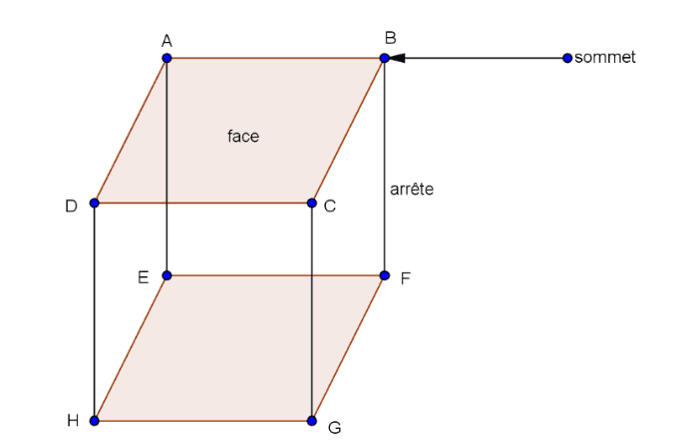
Un plan est illimité dans tous les sens. Il est représenté en général par un parallélogramme et se note par la lettre $\rm P$.
Un point est un lieu du plan qui n’a ni longueur ni épaisseur.
Pour marquer un point sur un plan, on met une croix et on écrit à côté une lettre majuscule correspondant au nom du point.
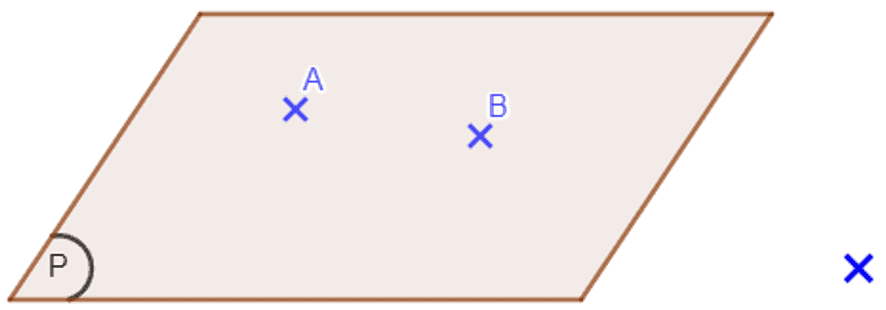
$\rm A$ appartient au plan $\rm (P)$ se note $\rm A \in (P)$. Un plan contient une infinité de points.
Une droite est une ligne droite illimitée « des deux côtés ».
On la représente par un trait droit.
Si un point $\rm B$ est sur une droite $\rm (D)$, on dit que le point $\rm B$ appartient à la droite $\rm (D)$ et on note $\rm B \in (D)$.
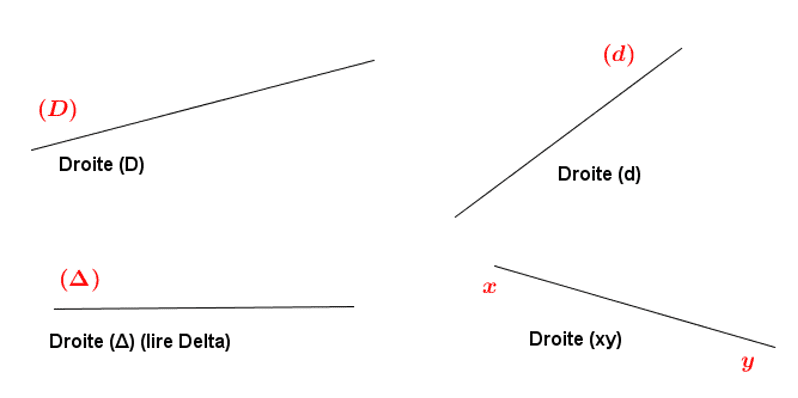
Autres notations d’une droite
PROPRIETE 1 : Par un point, il passe une infinité de droites.
PROPRIETE 2 : Par deux points, il passe une seule droite.
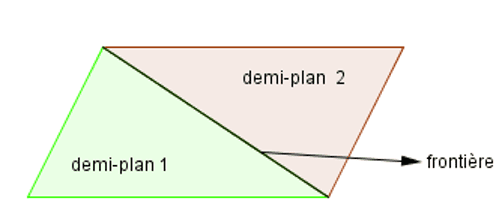
Une droite partage le plan en deux régions appelées demi-plans : la droite est la frontière entre les demi-plans.
Droites sécantes, droites disjointes, droites confondues, secteurs
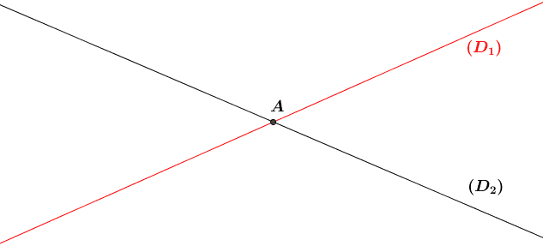
Le point $\rm A$ appartient à la droite $\rm(D_1)$ et à la droite $\rm (D_2)$ : on dit que le point $\rm A$ est le point commun aux deux droites $\rm (D_1)$ et $\rm (D_2)$.
On dit aussi que les droites $\bf \color{orange}{(D_1)}$ et $\bf \color{orange}{(D_2)}$ se coupent au point $\rm A$ ou que les droites $\bf\color{orange}{D_1)}$ et $\bf \color{orange}{D_2}$ sont sécantes en $\rm A$.
On note $\rm (D_1) \cup (D_2) = \{A\}$.
Le point $\rm A$ est le point d’intersection des deux droites $\rm (D_1)$ et $\rm(D_2)$.
Deux droites disjointes sont deux droites qui n’ont aucun point commun.
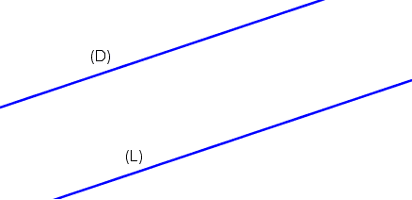
Les droites $\rm (D)$ et $\rm (L)$ sont disjointes.
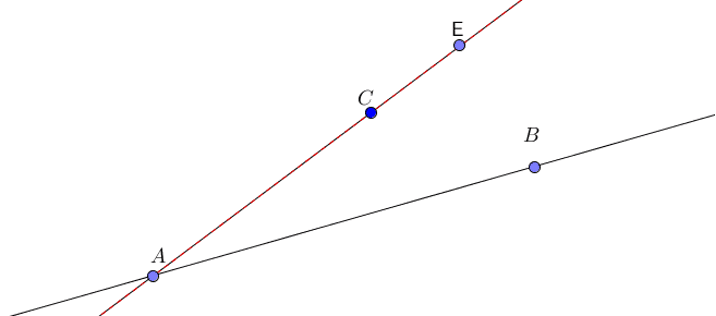
Les droites $\rm (AE)$ et $\rm (AC)$ forment une seule droite. On dit qu’elles sont confondues.
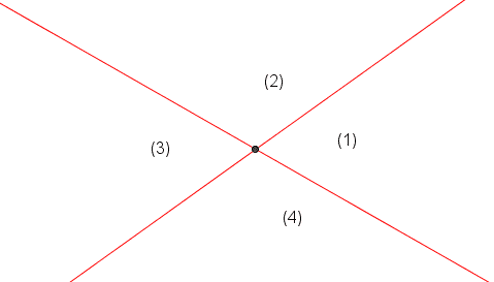
Deux droites sécantes partagent le plan en quatre secteurs.
Soit une droite $\rm (D)$ contenant les points $\rm A$ et $\rm B$.
La partie de la droite entre $\rm A$ et $\rm B$ est appelée segment d’extrémités $\rm A$ et $\rm B$. Elle est notée $\rm [AB]$ ou $\rm [BA]$. La droite $\rm (D)$ est le support de $\rm [AB]$.
Quand on prolonge le segment $\rm [AB]$ du côté de $\rm B$, on obtient une demi-droite $\rm [AB)$.
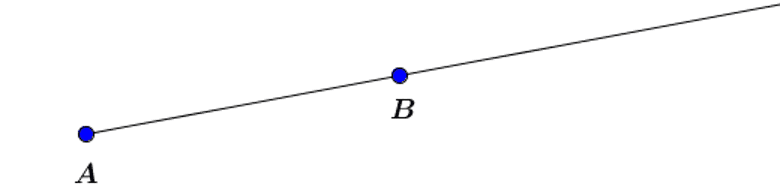
$\rm [AB)$ est la demi-droite d’origine $\rm A$ passant par $\rm B$.
$\rm [BA)$ est la demi-droite d’origine $\rm B$ contenant $\rm A$.
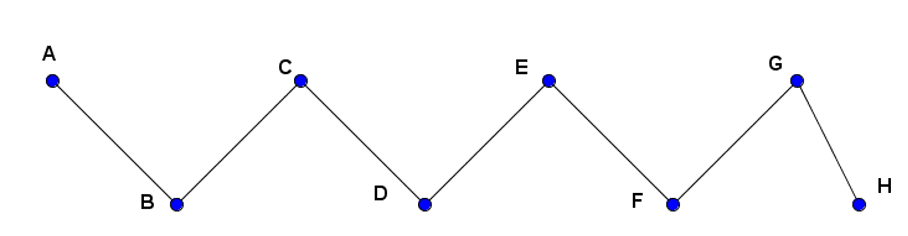
Une ligne brisée ouverte est appelée ligne polygonale. Elle est formée de segments. Pour nommer la ligne polygonale, on nomme successivement les extrémités des segments.
Exemple : la ligne polygonale $\rm ABCDEFGH$ ou $\rm HFEDCBA$.
Une ligne brisée fermée est appelée polygone. Les segments qui forment un polygone sont appelés côtés. Les extrémités des segments sont appelées sommets.
Exemple : Le polygone $\rm FGHIJ$.
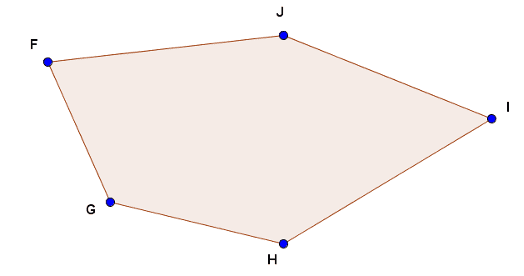
Les segments $\rm [FG]$, $\rm [GH]$, $\rm [HI]$, $\rm [IJ]$ et $\rm [JF]$ sont les côtés du polygone $\rm FGHIJ$.
Les points $\rm F$, $\rm G$, $\rm H$, $\rm I$ et $\rm J$ sont les sommets.
Les extrémités d'un même côté sont deux sommets consécutifs (par exemple $\rm F$ et $\rm G$ pour $\rm [FG])$.
Les côtés $\rm [FG]$, $\rm [GH]$ ayant une extrémité commune sont des côtés consécutifs.
Les côtés tels que $\rm [IJ]$ et $\rm [GH]$ n’ayant pas d’extrémités communes sont des côtés non consécutifs.
Les segments joignant deux sommets non consécutifs sont les diagonales du polygone (par exemple $\rm [JG]$, $\rm [JH])$.
