Rëdd yi ak xaaju rëdd yi amu ñu dayoo. Kènn manul natt sèniy guddaay. 

Ab dogit ay tomb yu dul jèx lay ëmb, waayé manèss na natt guddaay bi nékk ci diganté ay cettam, boo jëfëndikoo lu melni ab « règall » bu ñu maasska.

Guddaayu benn dogit $[\mathrm{AB}]$ mooy sorèwaay bi nékk ci diganté ñaari tomb yii $\rm A$ ak $\rm B$.
Guddaay bi di $\rm AB$ ab limm la. Da ñuy jëfëndikoo mbinndin wii di  $\rm AB$ ngir mandargaal guddaay gògu.
Dèssul binnd $[\mathrm{AB}]=7 \mathrm{~cm}$, waayé $\mathrm{AB}=7 \mathrm{~cm}$ wala book $[\mathrm{AB}]$ nattuwaayam mooy $7 \mathrm{~cm}$.

Benn benn yi ñuy nattè guddaay yi ñooy lii di « mètar » ak ay fŭlam ak ay xaajiti fŭlam : 
$$\begin{array}{llll} \bf km & \bf \Rightarrow & \textbf {kilomètar} \\ \bf hm & \bf \Rightarrow & \textbf {ectomètar} \\ \bf dam & \bf \Rightarrow & \textbf{décamètre} \\ \bf m & \bf\Rightarrow & \textbf {mètar} \\ \bf dm & \bf \Rightarrow & \textbf {décimètar} \\ \bf cm & \bf \Rightarrow & \textbf{centimètar} \\ \bf mm & \bf \Rightarrow & \textbf{milimètar}\end{array}$$

Bénnèlu nattukaayu guddaay bu nékk wu nékk mu ngi ëppè fukki yoon bi topp ci moom té yèes ko. 

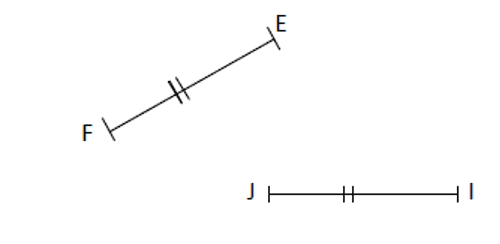
Ñaari rëdd yii di $[\mathrm{EF}]$ ak $[\mathrm{IJ}]$ ñoo tolloo guddaay ; ngir mandargaal lòlu, da ñuy ték ñaari araf yu gatt té nuroo ci sèn kow. Mooy li ñiy wooyè « xammèkaay ».

Ci nataal bu nékk, dèes na ñu raññè dogit yi yém guddaay ak benn xammèkaay bu ñu nuroolé.

Manèes na ñu jëfëndikoo ay xammèkaay yu bari té wûté (ñaari araf, ñetti araf, benn kurwaa, benn mbege su ndaw...) ngir woné né ay dogit ñoo tolloo guddaay.

Ab sètlu : Su ñaari dogit tolloo guddaay, da ñuy naan da ñoo yem képp.

Tomb $\rm I$ bi nekk ci kow dogit wii di $[\mathrm{AB}]$ té di ko xaaj ci ñaari dogit yu yémoo guddaay ñu ngi koy woowee diggu dogit bii di $\bf \color{orange}{[AB]}$.

Ci nataal bu nékk, dèes na ñu raññè dogit yi yém guddaay ak benn xammèkaay bu ñu nuroolé.

Na $\rm [AB]$ nék benn dogit té $\rm M$ nekk benn tomb bu maassalé gi.

  • Su $\rm M$ nekkè benn tomb bu $\rm [AB]$, konn da ñuy am : $\rm AM+MB=AB$
  • Su $\rm M$ nekkul benn tomb bu $\rm [A B]$, konn da ñuy am : $\rm AM+MB>AB$

Ab jaglé : Ci benn ñettikoñ, guddaayu wétt goo jël da fay yèes mboolantèk gudddayi yénèn ñaari wéttam yi.