Les droites et les demi-droites sont infinies, on ne peut pas les mesurer.
Un segment contient une infinité de points mais la distance entre ses deux extrémités peut être mesurée, par exemple avec une règle graduée.
La longueur d'un segment $[\mathrm{AB}]$ est la distance entre les deux points situés entre $\rm A$ et $\rm B$.
La longueur $\rm AB$ est un nombre. On utilise la simple écriture $\rm AB$ pour désigner cette longueur.
On n'écrira pas $[\mathrm{AB}]=7 \mathrm{~cm}$, mais $\mathrm{AB}=7 \mathrm{~cm}$ ou bien $[\mathrm{AB}]$ mesure $7 \mathrm{~cm}$.

Les unités de mesure des longueurs sont le mètre et ses multiples et sous-multiples décimaux :
$$\begin{array}{llll} \bf km & \bf \Rightarrow & \textbf {kilomètre} \\ \bf hm & \bf \Rightarrow & \textbf {hectomètre} \\ \bf dam & \bf \Rightarrow & \textbf{décamètre} \\ \bf m & \bf\Rightarrow & \textbf {mètre} \\ \bf dm & \bf \Rightarrow & \textbf {décimètre} \\ \bf cm & \bf \Rightarrow & \textbf{centimètre} \\ \bf mm & \bf \Rightarrow & \textbf{millimètre}\end{array}$$

Chaque unité de mesure de longueur est dix fois plus grande que celle qui lui est juste inférieure.

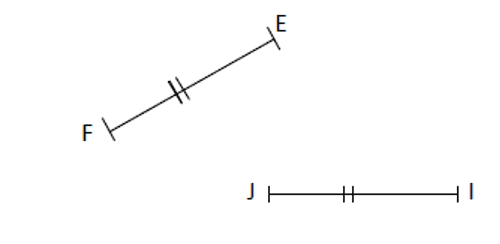
Les segments $[\mathrm{EF}]$ et $[\mathrm{IJ}]$ ont la même longueur ; on les marque du même signe : c'est le codage.

Sur un dessin, on repère des segments de même longueur par un même codage.

On peut utiliser de nombreux codages différents (deux traits, trois traits, une croix, un petit cercle...) pour signifier que des segments sont de même longueur.

Remarque : Si deux segments ont la même longueur, on dit qu'ils sont superposables.

Le point $\rm I$ se trouve sur le segment $[\mathrm{AB}]$ et qui le partage en deux segments de même longueur est appelé le milieu du segment $\bf \color{orange}{[AB]}$.

Le périmètre d'un polygone est égal à la somme des longueurs de ses cotés.

Soit un segment $\rm [A B]$ et $\rm M$ un point du plan.

  • Si $\rm M$ est un point de $\rm [A B]$, alors on a $\rm A M+M B=A B$
  • Si $\rm M$ n'est pas un point de $\rm [A B]$, alors on a $\rm A M+M B>A B$

Propriété : Dans un triangle, la longueur d'un côté est inférieure à la somme des longueurs des deux autres côtés.