I. Triangles

Un triangle est un polygone qui a trois côtés.
La figure ci-dessous est un triangle. On le note : $\rm A B C$ ou $\rm B C A$ ou $\rm C A B$.

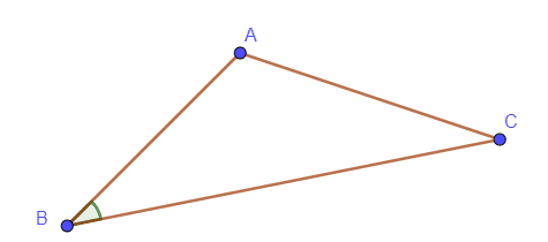
Les points $\mathrm{A}$, $\mathrm{B}$ et $\mathrm{C}$ sont ses trois sommets.
$\widehat{\rm A B C}$ est un angle du triangle. $\rm [AC]$ est le côté opposé à l'angle $\widehat{\rm A B C}$.
Les côtés $\rm [A B]$ et $[\mathrm{AC}]$ sont les côtés adjacents à l'angle $\widehat{\rm A B C}$.

Pour construire un triangle connaissant ses trois côtés :

• On trace le segment $\rm [BC]$ (par exemple)
• On trace un arc de cercle de centre $\rm B$ et de rayon $\rm A B$
• On trace un arc de cercle de centre $\rm C$ et de rayon $\rm A C$
• Les deux arcs de cercle se coupent en $\rm A$.

II. Droites remarquables

Bissectrice : Demi-droite partageant un des angles en deux angles de même mesure.

Hauteur : Droite passant par un sommet et perpendiculaire au côté opposé.

Médiatrice : Droite perpendiculaire à un côté en son milieu.

Médiane : Droite passant par un sommet et passant par le milieu du côté opposé.

III. Triangles particuliers

Triangle rectangle

Définition : Un triangle est dit rectangle lorsqu'il possède un angle droit. Le côté opposé à l'angle droit (le plus grand côté) s'appelle l'hypoténuse du triangle.

Propriété : Si un triangle est rectangle alors les deux angles adjacents à son hypoténuse sont complémentaires, c'est-à-dire que la somme de leurs mesures vaut $90°$.

Triangle isocèle

Définition : Un triangle est dit isocèle lorsqu'il possède deux côtés de même longueur. On précise en quel point il est isocèle (son sommet principal) ou sa base (le côté opposé à son sommet principal).

Propriétés : Si un triangle est isocèle alors les trois droites remarquables issues de son sommet principal et la médiatrice de la base sont confondues (elles forment l'axe de symétrie de ce triangle). Si un triangle est isocèle alors les deux angles adjacents à sa base ont même mesure.

Triangle équilatéral

Définition : Un triangle est dit équilatéral lorsqu'il possède trois côtés de même longueur.

Propriétés : Si un triangle est équilatéral alors les trois droites remarquables issues de chaque sommet et la médiatrice du côté opposé sont confondues (elles forment les trois axes de symétrie de ce triangle). Si un triangle est équilatéral alors ses trois angles ont une mesure de $60°$.

IV. Quadrilatères particuliers

Un trapèze est un quadrilatère non croisé dont deux côtés sont parallèles et deux côtés non parallèles.

Un trapèze rectangle est un trapèze qui a un angle droit.

Un trapèze isocèle est un trapèze qui a ses deux côtés non parallèles de même longueur. 

Tout trapèze isocèle admet un seul axe de symétrie, médiatrice de ses bases.

Le parallélogramme est un quadrilatère dont les côtés sont parallèles deux à deux.  

Un rectangle est un quadrilatère qui a quatre angles droits. 

Un rectangle admet deux axes de symétrie perpendiculaires. Ce sont les médiatrices de deux côtés consécutifs du rectangle.

Un losange est un quadrilatère qui a ses quatre côtés de même longueur. 

Un losange admet deux axes de symétrie perpendiculaires qui sont ses diagonales. 

Le carré est un quadrilatère qui a ses quatre côtés de même longueur et ses quatre angles droits. 

Un carré admet quatre axes de symétrie : les médiatrices de deux côtés consécutifs et les diagonales.

Remarque : Le rectangle, le losange et le carré sont des parallélogrammes.

Pentagone et hexagone réguliers

Un pentagone régulier est un polygone qui a cinq côtés de même longueur et cinq angles de même mesure.

Un hexagone régulier est un polygone qui a six côtés de même longueur et six angles de même mesure.