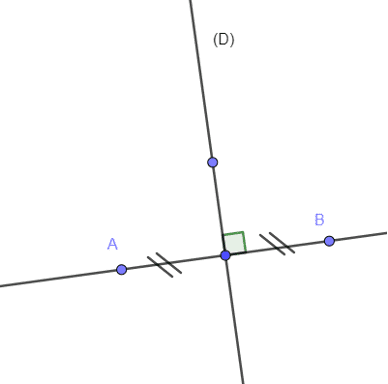
• Dire que deux points $\rm A$ et $\rm B$ sont symétriques par rapport à une droite $\bf \color{orange}{(D)}$ signifie que $\rm (D)$ est la médiatrice du segment $\rm [AB]$.
  • Tout point de la droite $\rm (D)$ est son propre symétrique par rapport à $\rm (D)$. 

  • Autres formulations :
    • Si $\rm A$ et $\rm B$ sont symétriques par rapport à une droite $\rm (D)$, on peut aussi dire que :
      • $\rm B$ est le symétrique de $\bf\color{orange}{A}$ par rapport à $\bf\color{orange}\Delta$ ou encore que $\rm A$ est le symétrique de $\rm B$ par rapport à $\Delta$.
    • Si $\rm P$ est un point de la droite $\Delta$, alors le symétrique de $\rm P$ est $\rm P$ lui-même.
    • Un point hors de $\Delta$ a son symétrique « de l’autre côté » de $\Delta$.
  • Construction : pour construire le symétrique d’un point ou d’une figure par rapport à une droite, on peut utiliser l’équerre et une règle graduée ou l’équerre et le compas.
  • Deux figures symétriques sont superposables, mais l'une est retournée par rapport à l'autre.
    Elles sont à la même distance de l'axe et ont la même inclinaison par rapport à l'axe. Une figure est symétrique si, lorsqu'on la plie en suivant l'axe de symétrie, les deux parties de la figure se superposent.
    Pour construire le symétrique d’une figure, on place d’abord les symétriques de plusieurs points de cette figure, puis on les relie.

  • Le symétrique d’un segment par rapport à une droite est un segment de même longueur.

  

  • Le symétrique d’un angle par rapport à une droite est un angle de même mesure.

  • Les symétriques de trois points alignés par rapport à une droite, sont trois points alignés.

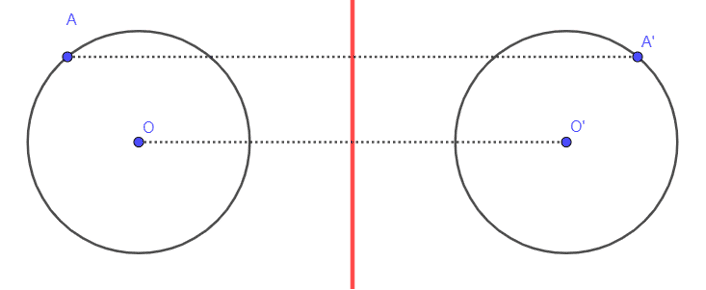
  • Le symétrique d’un cercle par rapport à une droite est un cercle de même rayon.