Puissances

📝 Mini-cours GRATUIT

Théorèmes et propriétés de géométrie - 2

Calcul littéral et équations

Proportionnalité - pourcentage - échelle

Calcul littéral, puissances

Fonctions linéaires et affines

Divisions

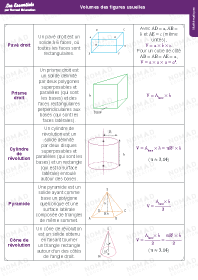
Volumes

Transformations géométriques

Proportionnalité et statistiques

Nombres et calculs

Aires et volumes

Triangles et parallélogrammes

Nombres relatifs et fractions

Théorèmes et propriétés de géométrie - 1

Périmètres, aires et volumes