Définition
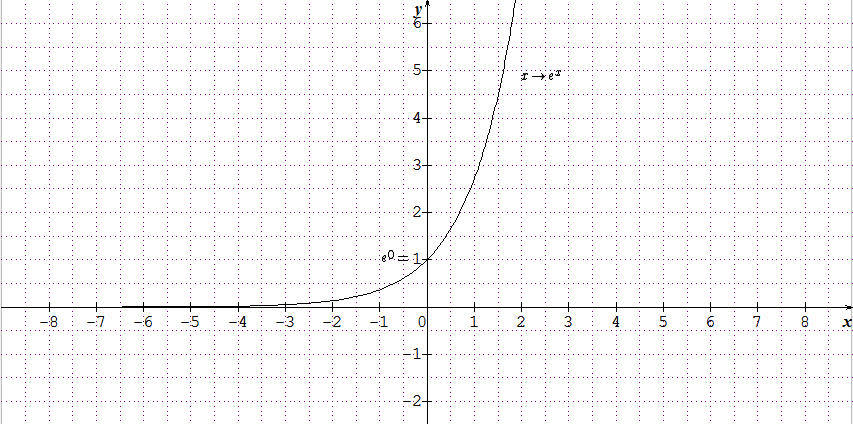
Pour a>0 fixé, la fonction exponentielle de base a est la fonction expa:x↦ax.
Elle est définie et positive sur R ; expa(0) = 1.
Elle est dérivable sur R et :
- pour 0 < a < 1, la fonction est décroissante sur R.
- pour a > 1, la fonction est croissante sur R.
Propriétés algébriques
Pour tous les x et y réels, et n entier relatif :
- ax+y=ax×ay ;
- ax−y=axay ;
- anx=(ax)n.
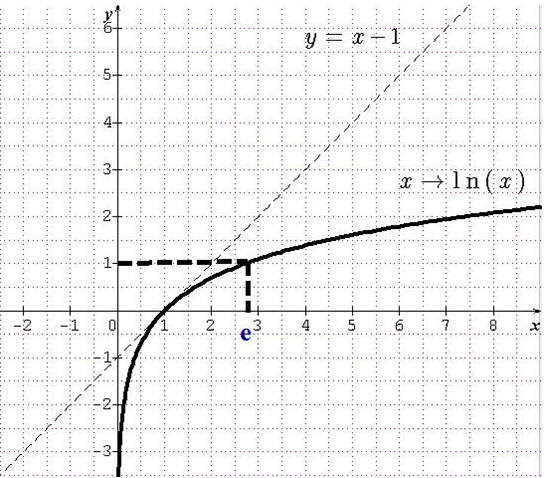
Représentations graphiques selon les valeurs de a>0
0<a=0,3<1 ; a=2>1