Modélisation d’une action mécanique par un vecteur force.
Définition d’une force et modélisation
Lorsqu’un objet exerce une action mécanique sur un autre, on dit qu’il exerce sur lui une force L’intensité d’une force se mesure à l’aide d’un dynamomètre.
L’unité de la force est le newton (N). On note souvent une force →F auteur / receveur
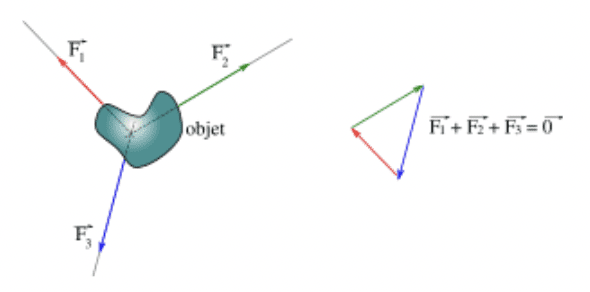
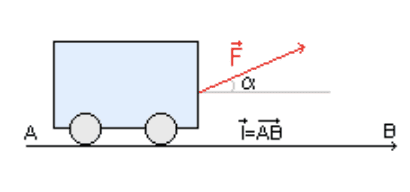
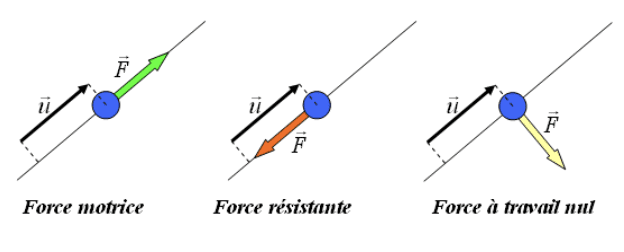
Une force est représentée par un vecteur qui possède 4 caractéristiques :
- Une direction : c’est la droite d’action de la force
- Un sens : C’est la flèche du vecteur qui l’indique (Pour une même direction, il peut y avoir deux sens possibles).
- Un point d’application : c’est l’endroit où s’applique la force.
- Une intensité : c’est une grandeur qui s’exprime en newton.
Poids et masse
La masse représente une quantité de matière qui ne varie pas. Elle s'exprime en kilogramme (kg) et se mesure à l'aide d'une balance.
Le poids d'un corps varie en fonction de sa position géographique et de l'altitude. C’est la force résultant de l’attraction gravitationnelle de la Terre sur tout ce qui est à sa surface ou proche de sa surface.
Il s'exprime en newton (N) et se mesure à l'aide d'un dynamomètre. Il existe une relation simple liant le poids et la masse d'un corps: P = m x g
avec :
- P : poids en N
- m : masse en kg
- g : intensité de la pesanteur en N/kg