Qu’est-ce qu’une solution ?

Une solution est un mélange homogène obtenu en dissolvant une substance solide dans de l’eau.

  • La substance dissoute s’appelle le soluté.
  • Le liquide (ici l’eau) dans lequel s’effectue la dissolution est le solvant.

Si l’eau est le solvant on parle de solution aqueuse.

  • Si le soluté contient des molécules on parle de solution moléculaire.
  • Si le soluté contient des ions (Cations ou Anions), on parle de solution ionique.

Concentration molaire

La concentration molaire (C) d’une solution est la quantité de matière exprimée en moles contenue dans un litre de solution. 

$\rm C = \dfrac{n}{V}$

Avec :

  • $\rm C$ la concentration molaire en $\rm mol.L^{-1}$
  • $\rm n$ la quantité de matière en $\rm mol$
  • $\rm V$ le volume en $\rm L$

Il est alors possible de retrouver la masse de soluté grâce à la relation :

$\rm n = \dfrac{m}{M}$

Avec :

  • $\rm n$ la quantité de matière en $\rm mol$
  • $\rm m$ la masse en $\rm g$
  • $\rm M$ la masse molaire moléculaire en $\rm g.mol^{-1}$

Dosage par titrage d’une solution

Le titrage est une méthode de dosage qui permet de déterminer la concentration d’une solution en la faisant réagir avec un réactif. 

1. Titrage colorimétrique

L’équivalence (lorsque tous les réactifs sont en proportions stœchiométriques) est déterminée par le changement de couleur de la solution à titrer.

Montage :

Si nous avons la réaction de titrage suivante :
$\rm aA + bB \rightarrow cC + dD$ à l’équivalence, nous avons versé un volume $\rm V_E$ se solution titrante :

$\rm \dfrac{n_A}{a} = \dfrac{n_B}{b}$

Le plus souvent, $a$ et $b$ valent 1. Nous avons donc :

$\rm C_A \times V_A = C_B \times V_E$ d’où $\rm C_A = \dfrac{C_B \times V_E}{V_A}$

2. Titrage conductimétrique

Le titrage conductimétrique est très proche du titrage colorimétrique. Cependant, le volume équivalent sera repéré par une courbe. Le dispositif de mesure s’appelle alors une cellule conductimétrique.

Montage :

Détermination du volume $\rm V_E$ : 

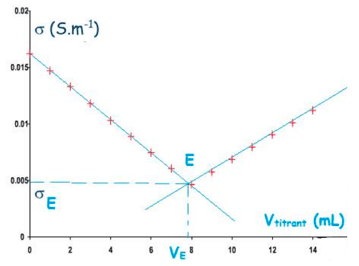
L’équivalence se trouve à l’intersection des deux droites. Il est possible d’utiliser la même relation que précédemment pour déterminer :

$\rm C_A = \dfrac{C_B \times V_E}{V_A}$