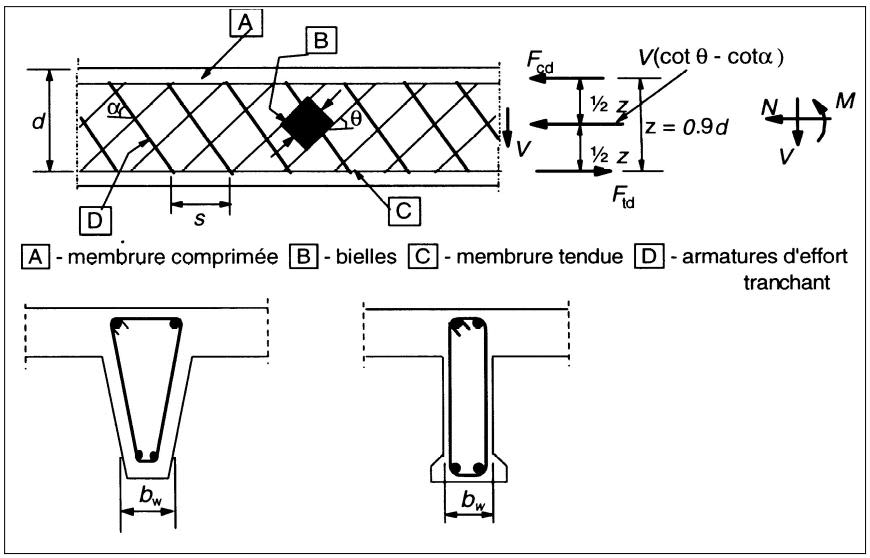
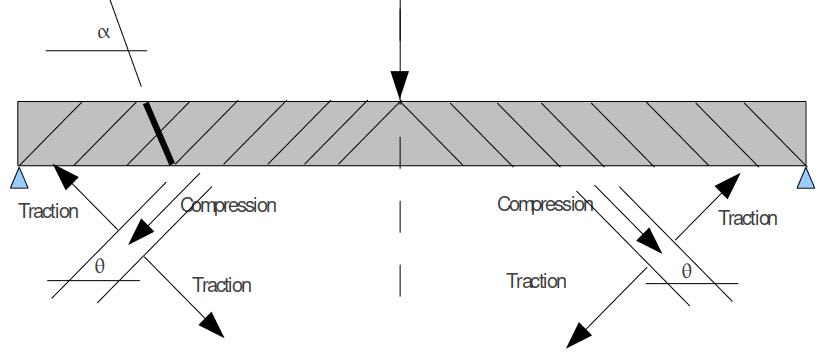
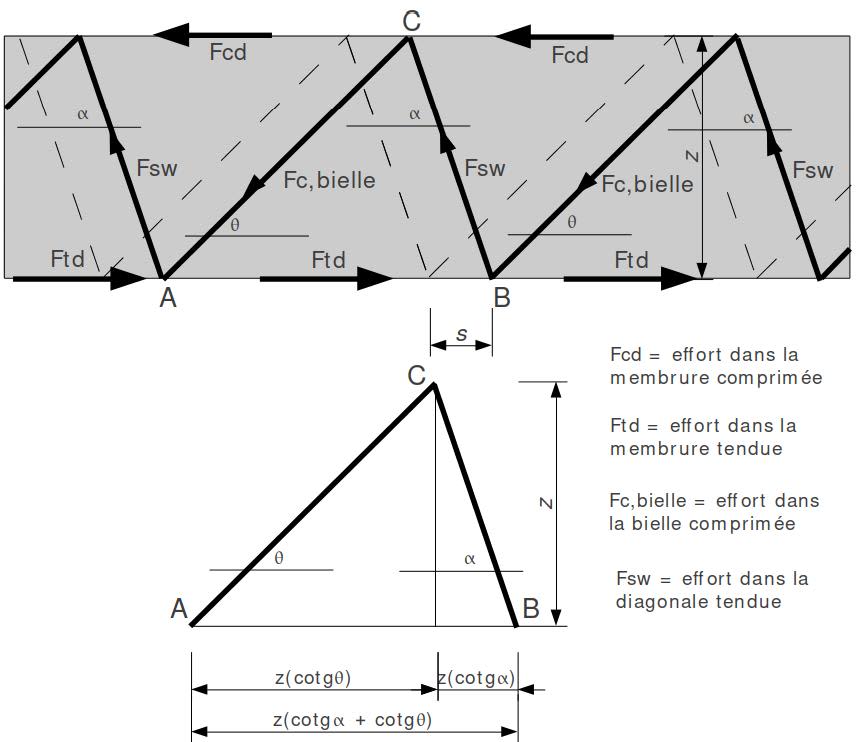
Effort tranchant maxi supporté par le béton pour $\theta θ < 45°$ :
$\rm V_{Rd,max} = \alpha_{cw}\mathcal b_w\mathcal{z\nu}_1 \mathcal{f_{cd}} \rm \dfrac{cot(\theta) + cot (\alpha)}{1+cot^2(\theta)}$
$v_1$ étant un coefficient réducteur de la résistance de l’âme de la poutre.
Pour les structures non précontraintes : $\rm \alpha_{cw} = 1$

Effet sur les armatures longitudinales tendues. Le fibre neutre est placée au milieu de la section. Pour « $n$ » mailles, nous aurons :
$\rm N+F_{cd}−F_{td}=\mathcal n(F_{c ,bielle} \cos(\theta)−F_{sw} \cos(\alpha))$ $= n\left(\frac{\rm V_{Rd,s}S \times \cos (\theta)}{z[\rm cot (\alpha) + cot (\theta)]\sin (\theta)} - \frac{\rm V_{Rd,s}S \times \cos(\alpha)}{z[\rm cot(\alpha) + cot (\theta)]\sin (\alpha)}\right)$
$\rm N + F_{cd} - F_{td} = \mathcal n\left(\frac{V_{Rd,s}S \times cot (\theta)}{\mathcal z [cot (\alpha) + cot (\theta)]} - \frac{\rm V_{Rd,s}S \times cot (\alpha)}{\mathcal z[cot(\alpha) + cot (\theta)]}\right)$ $= n\left(\frac{\rm V_{Rd,s}S \times (cot (\theta) - cot (\alpha))}{z[\rm cot (\alpha) + cot (\theta)]}\right)$
$n = z \dfrac{[\rm cot (\alpha) + cot (\theta)]}{\rm S} \Rightarrow \rm N + F_{cd}-F_{td}$ $= \rm V_{Rd,s}\times (cot(\theta) - cot(\alpha))$
$\rm F_{cd} = F_{td} \Rightarrow N = V_{Rd,s} \times (cot(\theta)-cot(\alpha))$
$\rm F_{td} \times \mathcal z = N \times \dfrac{\mathcal z}{2} \Rightarrow F_{td}$ $\rm = \dfrac{V_{Rd,s}}{2} \times (cot (\theta) - cot (\alpha))$
Cette valeur doit être rajoutée à l'effort de traction dans la fibre horizontale tendue, du au moment fléchissant. C'est la raison pour laquelle elle porte le nom de $\rm\Delta F_{td}$.
D’où : $\rm\Delta F_{td} = \dfrac{V_{Ed}}{2}\times (cot(\theta) - cot(\alpha))$
Il faut vérifier en toute section de la poutre, l'inégalité suivante :
$\rm F_{td} = \dfrac{M_{Ed}}{\mathcal z} + \Delta F_{td} \leq \dfrac{M_{Ed,max}}{\mathcal z}$ où $\rm M_{Ed,max}$ est le moment maximal le long de la poutre. Cela équivaut à considérer un décalage de la courbe enveloppe des moments fléchissants correspondant à un segment $\bf a_v$ tel que : $a_v = \dfrac{z}{2} \times (\rm cot (\theta) - cot (\alpha))$
Exemple de vérification au cisaillement d’une poutre en Té.
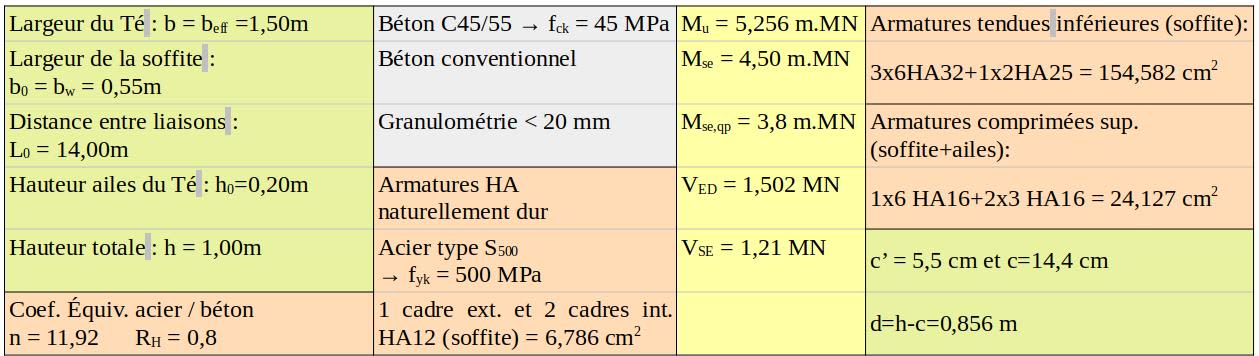
$\rm \theta = 21,8° \Leftrightarrow cot(\theta)=2,5$
$\rm \theta = 45° \Leftrightarrow cot(\theta)=1$
$\Rightarrow 21,8° \leq \theta \leq 45°$ $\rm \Leftrightarrow 1\leq cotg \theta \leq 2,5$
La valeur obtenue avec $\rm cotg(\theta) = 2,5$ nous la valeur mini de l’effort tranchant maxi.
$\mathrm{V_{Rd,max}} = \alpha_{cw}b_{w}z\nu_1f_{cd}\dfrac{\rm cot(\theta)+cot(\alpha)}{\rm 1 + cot^2(\theta)}$
$\rm V_{Rd,max} = 1 \times 0,55 \times (0,9 \times 1,00)$ $\times$ $\left[0,6 \times \left(1 - \frac{45}{250}\right)\right] \times \left(\frac{1\times 45}{1,5}\right) \times \left[\frac{2,5 + 0}{1+ 2,5^2}\right]$
$\rm V_{Rd,max} = 2,519~MN$
En faisant $\rm cot(\theta)= 1$, on obtient $\rm 3,653~MN$.
$\rm V_{se} = 1,502~MN < V_{Rd,max} = 2,519~MN$ $\Rightarrow \text{OK pour cot}(\theta)=2,5$
Si cette condition n'était pas vérifiée, il aurait fallu calculer $\theta$ en faisant $\rm V_{se} = V_{Rd,max}$, en vérifiant $\rm cot(\theta) \geq 1$.
Évaluation de l’espacement des cadres . Avec $z = 0,9d$ $\rightarrow \rm A_{sw} \geq \frac{V_{Rd,s}S}{\mathcal f_{ywd}\mathcal z [cot(\alpha) + cot (\theta)]\sin (\alpha)}$
$\rm S \leq \dfrac{6,786 \times 10^{-4}}{1,502} \times \left(\dfrac{500}{1,15}\right)$ $\times$ $(0,9 \times 0,856) \times (0+2,5 \times 1)$
$\rm S \leq 0,378~m$
L'effort tranchant impose de vérifier les armatures longitudinales ancrées au droit de l'appui.
$\rm N=V_{Rd ,s}\times (cot(\theta)−cot(\alpha))$ $\rm =1,502\times (2,5−0) = 3,755~MN$
$\Rightarrow \rm A \geq \dfrac{3,755}{\left(\frac{500}{1,15}\right)} = 0,008637~m^2$ $\rm = 86,37~cm^2$
On laissera deux lits de $\rm 6~ HA~ 32$ $\rm (96,51~cm^2)$ afin de garantir au moins cette section. On remarquera l’effet accentué sur les aciers longitudinaux à cause de la forte inclinaison des bielles.