La figure 5-7 (extraite du règlement) propose les élancements définis dans l'EC2, et fournit les longueurs de flambement en fonction des liaisons adoptées aux extrémités du poteaux. Ces schémas ne sont valables que pour des éléments isolés (fréquents dans les ouvrages d'art).
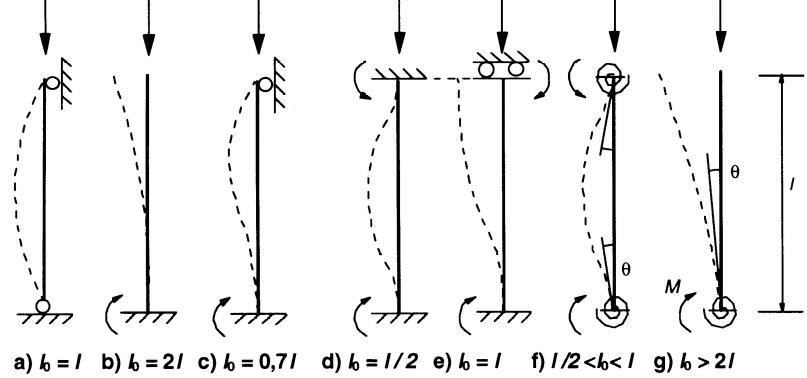
Pour les bâtiments et certains ouvrages d'art, les liaisons d'extrémités ne peuvent pas être schématisées si simplement. Nous distinguerons donc deux cas :
- Les éléments isolés.
- Les poteaux inclus dans des systèmes type portique.
Pour ces deux cas, il faut d'abord vérifier si l'élancement du poteau dans son contexte, n'engendrera pas d'effet du second ordre (moment fléchissant supplémentaire lié au déplacement de la fibre neutre par rapport à l'axe de transmission des efforts normaux). Le flambage doit rester très faible pour qu'il soit négligeable.
Éléments isolés
Lorsque l'élancement ne dépasse pas la valeur définie par les expressions ci-dessous, les effets du second ordre peuvent être négligés (5.13 N)λlimite=20ABCn avec :
A=1(1+0,2φef) si φef n'est pas connu, prendre A=0,7, B=√1+2ω si ω n'est pas connu, prendre B=1,1 et C=1,7−rm si rm n'est pas connu, prendre C=0,7.
φef= coefficient de fluage effectif, calculé lorsque l’on évalue le coefficient d’équivalence « n ».
ω=AsfydAcfcd ratio mécanique d'armatures. As est l'aire totale de la section des armatures longitudinales parallèles à l’axe du poteau.
n=NedAcfcd effort normal relatif et rm=M01M02 rapport des moments.
M01 et M02 sont les moment d'extrémité du 1er ordre, avec |M02|≥|M01|.
Dans le cas d'une flexion déviée, il convient de vérifier séparément dans chaque direction. Exemple d’application. Poteau de portique de section b×h.
RH=80%=0,8
Dimensions b=30 cm et h=30 cm, section Ac=900 cm2.
Hauteur réelle du poteau : 4,50 m
Poutre de section verticale 40×30 cm=1 200 cm2, longueur 6,00 m.
Longrine de fondation en pied de poteau, section 60×60 cm=3 600 cm2, longueur 6,00 m.
Armatures verticales du poteau : 4 HA 25 (As=19,63 cm2) placés dans les angles à 5 cm de chaque parement Un cadre HA 6 tous les 30 cm.
fyk=500 Mpa et Es=200 Gpa=200 000 MPa.
fck=30 MPa, Classe normale (N).
Ecm=33 Gpa=33 000 Mpa (EC2, tableau 3.1)
Chargement du béton à 50 jours de durcissement.
NEd=2,00 MN=2 000 kN
NEqp=2,50 MN=2 500 kN
M01=0,020 MN.m=2 000 m.daN (en-tête)
M02=0,022 Mn.m=2 200 m.daN (en-pied)
MEqp=0,011 Mn.m=1 100 m.daN (en-pied)
Calculs préliminaires :
Ratio d'aciers longitudinaux : ρ=AsAc=0,0218=2,18%
φef= coefficient de fluage effectif (voir méthode avec « n ») dépend de φ(t=∞,t0)=1,628
Il convient de calculer la longueur de flambement du poteau :
k1 et k2 sont les souplesses relatives aux encastrements partiels aux extrémités (en-tête et en-pied).
ki=ΘM×EIl




