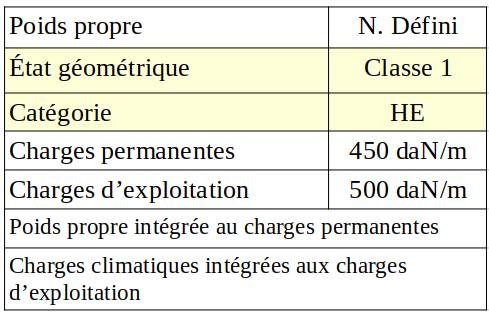
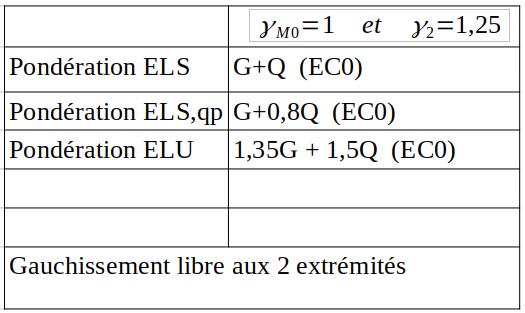
Vérification du risque de voilement de l’âme au droit des appuis.
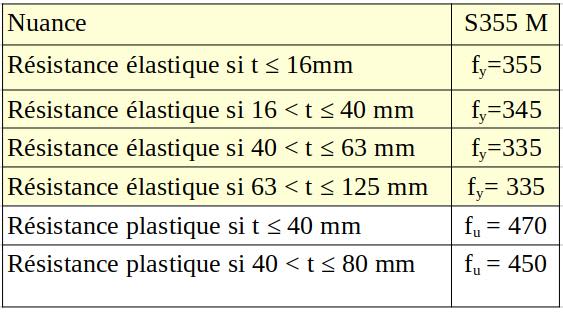
$\varepsilon = \sqrt{\dfrac{235}{f_y}} = \sqrt{\dfrac{235}{355}} = 0,813$
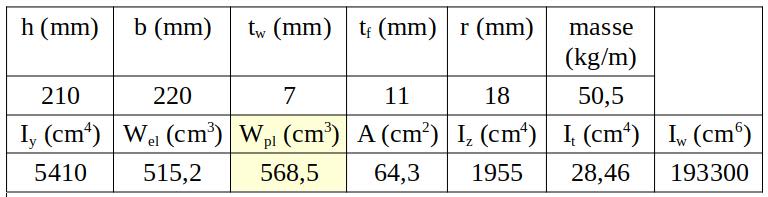
$\Rightarrow$ Si $\dfrac{h_w}{t_h} = \dfrac{200}{7} = 28,57 > ~? ~72 \dfrac{\varepsilon}{\eta}$ $= \dfrac{72\times 0,813}{1,2}=48,78$
$\rm \Rightarrow NON \Rightarrow$ pas de renforcement de l'âme.
Vérification du risque de déversement. Poutres symétriques.
Si les moments aux extrémités sont différents $\rm M_1 \geq M_2 = \Psi M_1$ avec $−1\leq \Psi \leq+1$ et/ou la sollicitation en flexion simple, alors :
$\mathrm M_{cr} = C_1 \times π^2 \dfrac{\rm EI}{(k_z\rm L)^2}$ $\scriptstyle\left[\sqrt{\left(\frac{k_z}{k_w}\right)^2\times \frac{\mathrm I_w}{\mathrm I_z} + (k_z\mathrm L)^2 \times \left(\frac{\mathrm{GI}_t}{\pi^2\mathrm{EI}_z}\right) + (\mathrm C_2 z_g − \mathrm C_3 z_j)^2} − (\mathrm C_2 z_g − \mathrm C_3 z_j)\right]$
Avec :
Moment d’inertie de gauchissement $(\rm m^6, cm^6$ ou $\rm mm^6)$ $\mathrm I_w = \beta (1−\beta)$ $\mathrm I_z h_s^2$ avec $\beta_f = \dfrac{\mathrm I_{f_c}}{\mathrm I_{f_c}\mathrm I_{f_t}}$
- $h_s =$ distance entre les centres de torsion/cisaillement des semelles sup. et inf. $(h - t_f)$.
Les centres de torsion/cisaillement des semelles sont sont à la demi épaisseur de celles-ci.
- $\mathrm I_{f_c} =$ moment quadratique de la semelle comprimée.
- $\mathrm I_{f_t} =$ moment quadratique de la semelle tendue
Pour une section rectangulaire pleine, le centre de torsion est confondu avec le CDG.
- $z_g =$ distance du point d’application de la charge au centre de torsion (différent du CDG et signe + si la charge agit vers le centre de torsion).
$z_g=z_a−z_s$ avec $z_s =$ coordonnées du centre de torsion et $z_a =$ coordonnées du point d’application de la charge.
Pour une section symétrique $\rightarrow z_j = z_s - \left[\dfrac{0,5}{\mathrm I_y} \times \displaystyle \int_{\rm A} z (y^2 + z^2) d\mathrm A\right] = 0$ si elle est doublement symétrique (mêmes semelles en haut et en bas, $\rm H$ ou $\rm I$).
Dans ce cas, nous aurons : $\beta_f = \dfrac{\mathrm I_{f_c}}{\mathrm I_{f_c}\mathrm I_{f_t}} = 0,5$ $\Rightarrow$ $\mathrm I_w=\beta (1−\beta) \mathrm I_z h_s^2 = \dfrac{\mathrm I_z}{4} \times (h - t_f)^2$
Si $k_z=k_w=1 \Rightarrow \rm C_1$ $= \dfrac{1}{\sqrt{(0,325+0,423\Psi+0,252\Psi^2)}} \leq 2,6$ uniquement pour les moments d’extrémité $\rm (C_2 = C_3 = 0)$.
Facteurs réducteurs de la longueur de déversement :

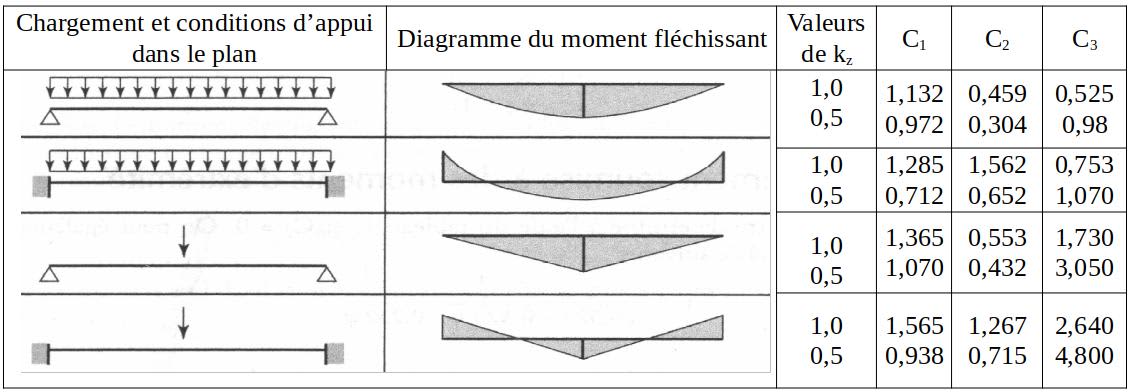
Dans le cas général, il convient de consulter les tableaux F.1.1
(moments d’extrémité) et F.1.2
(chargement en travée) de l’EC3 pour avoir les valeurs de $\rm C_1$ (lié aux aux moments d’extrémité), $\rm C_2$ (lié à la position de la charge) et $\rm C_3$ (lié à la liaison latérale).
Pour notre exemple, $\rm C_1 = 1,132, C_2 = 0,459, C_3$ inutile, car $z_j = 0$, $z_g = 105~\rm mm$, $k_w = k_z = 1$.
Et $\scriptstyle\mathrm M_{cr} = \mathrm C_1\times \pi^2 \frac{\mathrm{EI}_z}{(L)^2}\left[\sqrt{\frac{\mathrm I_w}{I_z} + \mathrm L^2 \times \left(\frac{\mathrm{GI}_t}{\pi^2\mathrm{EI}_z}\right) + (\mathrm C_2 z_g)^2} − (\mathrm C_2 z_g)\right]$ avec $\rm G = \dfrac{E}{2(1+ \mathcal v)} = 80 770~MPa$.
$\scriptstyle \mathrm M_{cr} = 1,132\times \frac{\pi^2 \times 210~000\times 1~955\cdot 10^{−8}}{10^2} \times$ $\scriptstyle\left[\sqrt{\frac{0,1933\cdot 10^{-6}}{1~955\cdot 10^{-8}} + \frac{10^2\times 8~0770\times 28,46\cdot 10^{−8}}{\pi^2 \times 210~000 \times 1~955\cdot 10^{−8}} + (0,459\times 0,105)^2}\right.$ $\scriptstyle − 0,459\times 0,105\big]$
$\rm M_{ED} = 0,16975~m. MN > M_{\cal cr}=0,098~ m. MN \rightarrow$ risque de déversement.
Encastrement bidirectionnel : $k_z = k_w = 0,5$
$\scriptstyle \mathrm M_{cr} = \rm C_1\times \pi^2 \frac{\mathrm{EI_z}}{\rm 0,5L)^2}\left[\sqrt{\frac{\mathrm I_w}{\mathrm I_z} + L^2 \times \left(\frac{\mathrm{GI_t}}{\pi^2 \mathrm{eI}_z}\right) + (\mathrm C_2 z_g)^2} − (\mathrm C_2 z_g)\right]$ ce qui multiplie par $4$ le moment critique $\rightarrow \mathrm M_{cr} = \rm 0,392~m.MN > M_{ED} \rightarrow OK$
Dans le cas d’une réalisation « sur mesure » on peut avoir besoin des expressions des critères géométriques de dimensionnement pour des section $\rm H$ ou $\rm I$ (extrait du catalogue Arcelor). Aire de la section transversale (unités usuelles en $\rm m^2$, $\rm cm^2$ ou $\rm mm^2$). $\mathrm A = 2t_f b +(h−2t_f)\times t_w + (4−\pi) \times r^2$
Moments quadratiques de flexion. (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$)
$\mathrm I_y = \dfrac{1}{12} \times [bh^3 −(b−t_w)\times (h−2 t_f)^3]$ $+$ $0,03 r^4 + 0,2146 r^2 (h−2t_f−0,4468r)^2$
$\mathrm I_y = \dfrac{1}{12} \times [2t_f b^3 +( h−2t_f) t_w^3] + 0,03r^4$ $+$ $0,2146 r^2 (t_w + 0,4468 r)^2$
Module de flexion plastique (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$) : $\mathrm W_{pl, y} = t_w\dfrac{h^2}{4} + (b−t_w) (h − t_f) t_f$ $+$ $\left(\dfrac{4−\pi}{2}\right)r^2(h−2t_f)+\left(\dfrac{3\pi^−10}{3}\right)r^3$
Modules de flexion élastique (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$) : $\mathrm W_{el, y} = 2\dfrac{\mathrm I_y}{h}$ et $\mathrm W_{el, z} = 2\dfrac{\mathrm I_z}{b}$
Moment quadratique de torsion (unités usuelle en $\rm m^4$, $\rm cm^4$ ou $\rm mm^4$)
$\mathrm I_t = \dfrac{2}{3} \times (b−0,63t_f)\times t_f^3 + \dfrac{1}{3}\times (h−2t_f)\times t^3_w + 2 \times \left(\dfrac{t_w}{t_f}\right)$ $\times$ $\left(0,145+0,1\times \dfrac{r}{t_f}\right)$ $\times$ $\left[ \dfrac{\left(r + \frac{t_w}{2}\right)^2 +(r+t_f)^2}{2r+t_f}\right]^4$