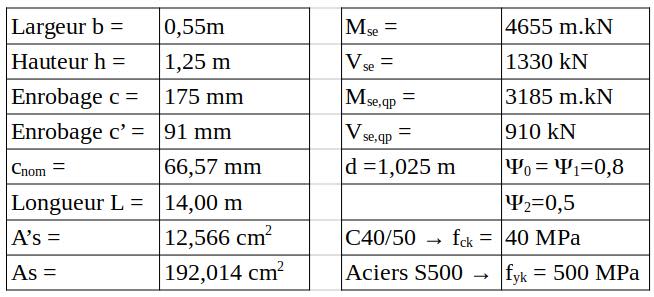
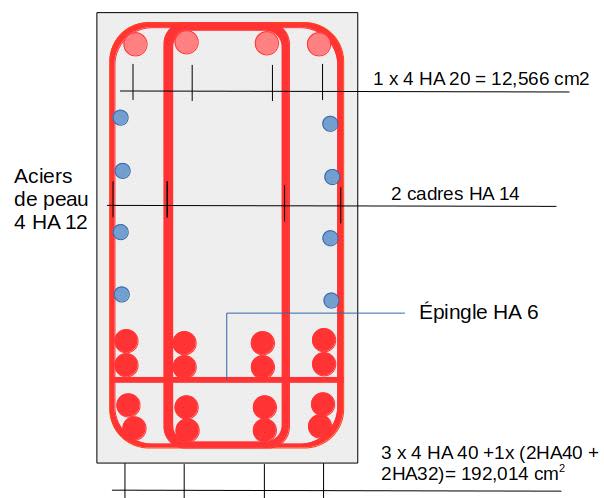
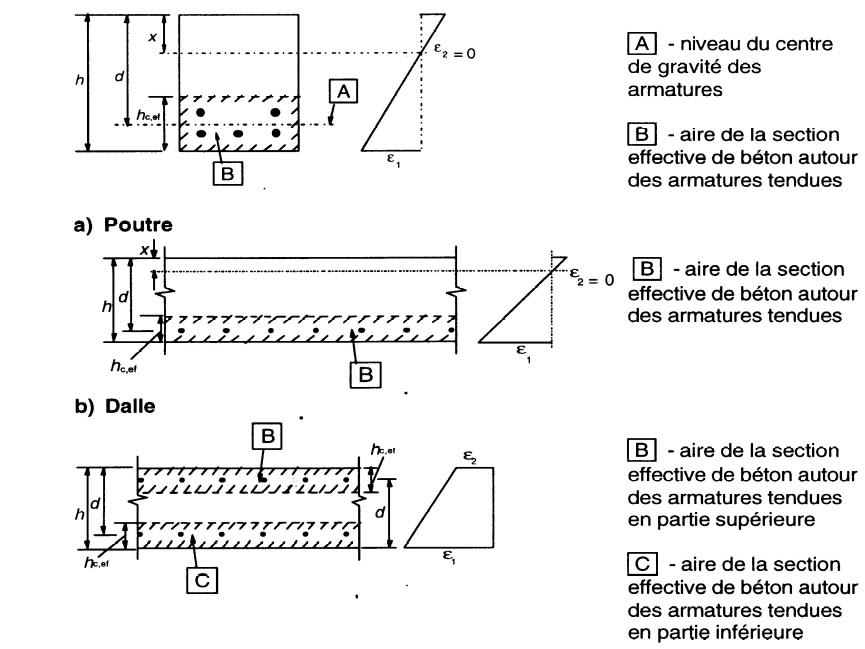
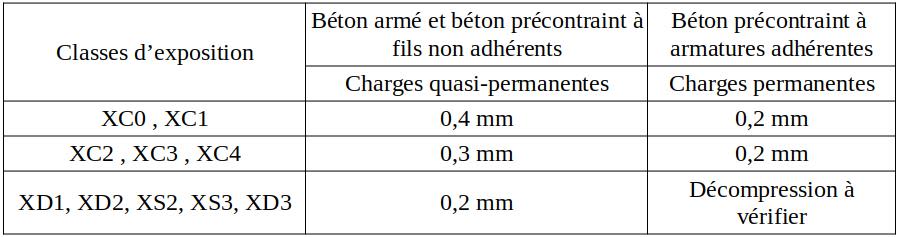
La vérification d’une poutre aux ELS se fait dans le domaine élastique et respecte les lois de la RDM, notamment la loi de Hooke σs=Esεs σc=Ecεc. Il est nécessaire d’homogénéiser le béton et les armatures en un seul matériau équivalent. Le coefficient d’équivalence « n » acier / béton en est le moyen mathématique. L’ annexe nationale (AN) de l’EC2 fournit la méthode. Les formules ci-après doivent être calculées dans l’ordre chronologique de façon à ce qu’elles soient toutes calculables.
fcm=fck+8→α1=[35fcm]0,7
α2=[35f]0,2 α3=[35fcm]0,5
Calculer Ac et u, la section de béton et son périmètre humide, puis calculer le rayon humide moyen en mm.
h0=2Acu
Puissance dépendant du type de ciment :
α=−1 classe S α= 0 classe N α= +1 classe R
Modification de l'âge du chargement :
t0,T= âge du béton au moment du chargement, en jours :
t0=t0,T×(92+t0,T+1)α≥0,5
Coefficient dépendant de l'humidité relative RH compris entre 0 (0%) et 1 (100%).
fcm≤35⇒βH =1,5×[1+(1,2RH)18]×h0+250
fcm>35⇒βH =1,5×[1+(1,2RH)18]×h0+250α3
t = âge du béton à l'instant considéré, en jours
t–t0 = durée non ajustée du chargement, en jours Coefficient du fluage avec le temps, après chargement : βc(t,t0)=[t−t0βH+t−t0]0,3
Facteur d'influence d'âge du béton au moment du chargement : β(t0)=10,1+t0,200
Facteur tenant compte de l'humidité relative sur le coefficient de fluage conventionnel :
fcm≤35⇒ΦRH=1+1−RH0,1×3√hø
fcm>35⇒ΦRH =[1+1−RH0,1×3√h0×α1]×α2
Facteur tenant compte de la résistance du béton sur le coefficient de fluage conventionnel : βfcm=16,8√fcm
Coefficient de fluage conventionnel : Φ0=ΦRHβ(fcm)β(t0)
Coefficient de fluage : Φ(t,t0)=Φ0βc(t,t0)
Pour obtenir le coefficient de fluage au temps infini, il suffit de donner comme valeur : t=70 ans=25 568 jours.
Φ∞,t0=Φ(t=25 550,t0)→Φc,eff=Φ∞,t0
Le module d'Young du béton s'écrit : Ec,eff=Ecm1+Φc,eff
Le module Ecm dépend des granulats.
Granulats de quartzite : Ecm=Ecm,quartsite=22 000×(fcm10)0,3
Granulats de calcaire : Ecm,calcaire=0,9×Ecm,quartsite
Granulats de grès : Ecm,grès=0,7×Ecm,quartsite
Granulats de basalte : Ecm,basalte=1,2×2Ecm,quartsite
Enfin, le coefficient d'équivalence acier / béton s'écrit : n=EsEc,eff