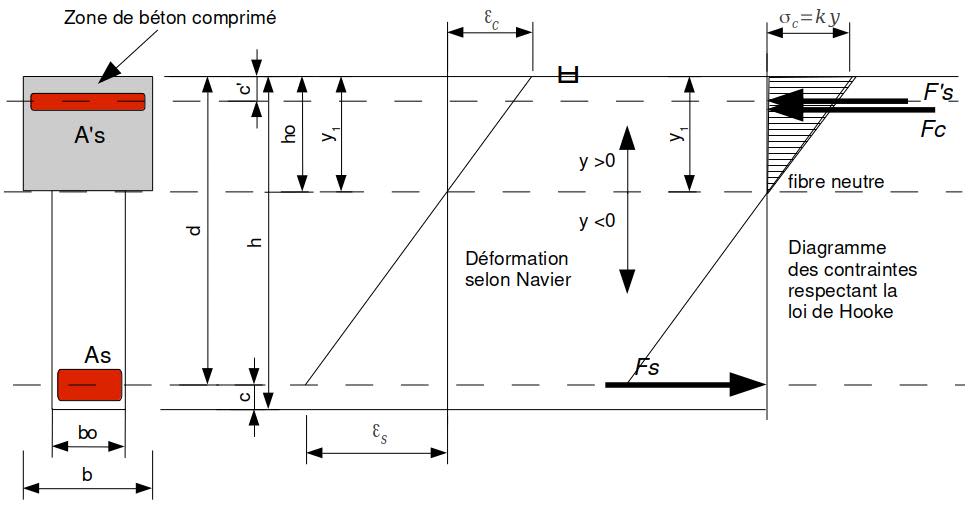
Contraintes dans la poutre :
$\sigma_c = \dfrac{\rm M_S}{\rm I_1} y_1 = \dfrac{241}{0,048568} \times 0,211$ $=10,47~\mathrm{MPa} < 0,6f_{ck}$ $\rm =30~MPa \Rightarrow OK$
$\sigma'_s = \dfrac{\rm M_S}{\rm I_1} (y_1 - c')$ $= \dfrac{12,3\times 2,41}{0,048568} (0,211−0,039)$ $=105~\mathrm{MPa} \leq 0,8f_{ck}$ $\rm = 400~MPa \Rightarrow OK$
$\sigma_s = \dfrac{\rm M_S}{\rm I_1} (d-y_1)$ $= \dfrac{12,3\times 2,41}{0,048568} \times (0,691 - 0,211)$ $= 293~\mathrm{MPa} \leq 0,8f_{ck}$ $\rm =400~MPa \Rightarrow OK$
Vérification à la flèche :
Pour une charge uniformément répartie sur toute la longueur de la poutre la flèche vaut (RDM) :
$\dfrac{5 pl^4}{384 \rm EI} = \dfrac{5 \mathrm Ml^2}{48 \rm EI} = \dfrac{\mathrm Ml^2}{9,6 \rm EI}$ avec $\rm E = E_{c,eff} = 16~259~MPa$ (calculé en même temps que $n$).
Le moment quadratique est calculé pour la section fissurée : $y_1=0,211\rm m$ et $\rm I_1 = 0,048568~m^4$
Comme la déformée commence avant que la poutre ne se fissure, il faut aussi les caractéristiques de la section non fissurée (tout le béton travaille).
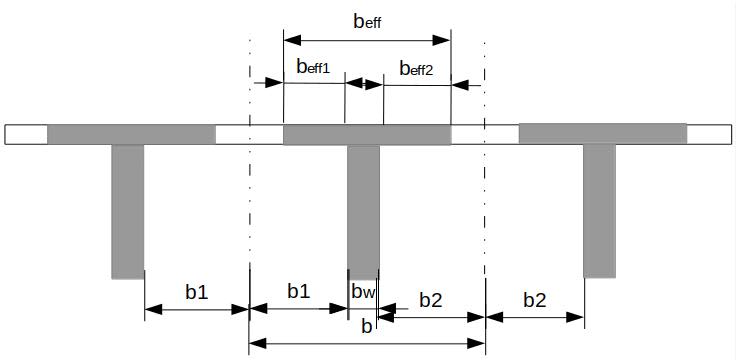
Moment statique : $b_0h\left(\dfrac{h}{2} − y_1\right) + (b−b_0) h_0 \left(y_1−\dfrac{h_0}{2}\right)$ $+$ $n \mathrm A'_s (y_1 - c') - n\mathrm A_s (d - y_1) = 0$ $\Rightarrow y1=0,122~\rm m$
Moment quadratique : $\mathrm{I_{1 NF}} = \dfrac{b_0h^3}{12} + b_0h \left(\dfrac{h}{2} - y_1\right)^2$ $+$ $(b-b_0)h_0 \left(y-1 - \dfrac{h_0}{2}\right)^2$ $+$ $(b - b_0)\dfrac{h^3_0}{12} + n\mathrm A'_s (y_1 - c')^2 + n\mathrm A_s (d-y_1)^2$ $\rm = 0,070692~m^4$
Moment limite avant fissuration du béton. $f_{ct,\rm eff} = 4,1~\rm MPa$ (voir tableau du cours) $\rightarrow \sigma_{sr} = nf_{ct,\rm eff} = 12,3\times 4,1 = 50,43~\rm MPa$
$\mathrm{M_{CR}} = \dfrac{\rm I_{1NF}\sigma_s}{n (d-y_1)}$ $= \dfrac{0,070692 \times 50,43}{12,3 \times (0,692 - 0,122)}$ $= 0,509373~\rm m.MN$
La flèche de la poutre non fissurée vaut ; $\alpha | = \dfrac{\mathrm{M_{CR}}l^2}{9,6\mathrm E_{c,\rm eff}\rm I_{1NF}}$ $=\dfrac{0,509379 \times 10^2}{9,6 \times 16~259 \times 0,070692}$ $= \rm 0,00462~m = 0, 462~cm$
Après fissuration : $\alpha \| = \dfrac{\mathrm M_{se,qp}l^2}{9,6\mathrm E_{c, \rm eff}\rm I_1}$ $= \dfrac{1,9 \times 10^2}{9,6 \times 16~259 \times 0,048568}$ $\rm = 0,0251~m = 2,51~cm$
Évaluation des pondérations des deux flèches :
$\beta =0,5 \Rightarrow \zeta = 1−\beta \left(\dfrac{\sigma_{sr}}{\sigma_s}\right)$ $= 1 - 0,5 \times \left(\dfrac{50,43}{293}\right)^2 =0,985$ $\Rightarrow \alpha = \zeta \alpha\| +(1-\zeta)\alpha|$ $=\rm 0,0248~m = 2,48~cm$
Flèche admissible : $\dfrac{l}{500} = \dfrac{10}{500} = \rm 0,02~m = 2~cm$ $\rm \Rightarrow \alpha = 2,48 > 2~cm \Rightarrow$ la flèche admissible n' est pas respectée.
Solutions envisageables :
- Augmenter les sections d’acier. Problème, il y en a déjà beaucoup pour la place disponible en zone tendue.
- Augmenter la hauteur de la poutre, afin d’augmenter le moment quadratique. Il faut l’accord de l’architecte et respecter la hauteur sous plafond disponible.
- Faire une contre-flèche par précontrainte ou par la forme initiale du coffrage. Mais attention à l’ouverture des fissures. La vérification se fait de la même manière que pour une poutre de section rectangulaire.
![]()



