Thermodynamique

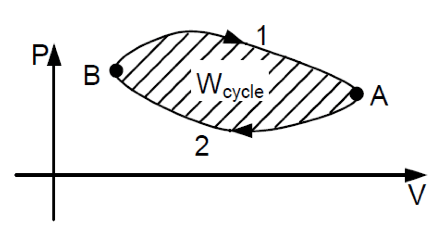
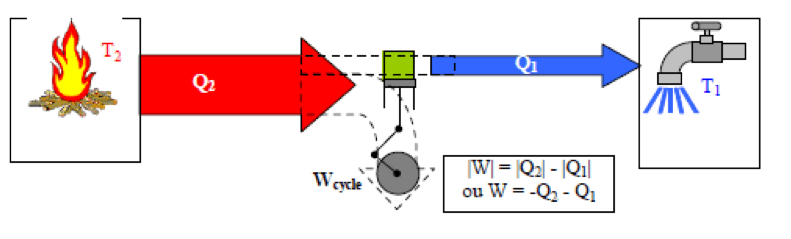
La thermodynamique permet d’étudier, entre autres, le déplacement d’un corps soumis à la chaleur (ex : moteurs thermiques) ou inversement, la chaleur captée ou rejetée par un corps soumis à une déformation ou un déplacement (ex : climatisation)
Les transformations thermodynamiques provoquent une variation soit de T°, soit de pression, soit de volume du système considéré. Ces grandeurs sont liées par un certain nombre de relations.

Loi des gaz parfaits 

$P.V = n.R.T$

Notions importantes

Différence entre chaleur et température
Un corps n'a pas une quantité de chaleur $Q$ déterminée (contrairement à la température) : la quantité de chaleur perdue ou gagnée est fonction des corps ou systèmes avec lesquels il interagit et en fonction du type de transformation. 

Quantité de chaleur $Q$
Elle est égale à la variation d'énergie thermique du corps.
Si $tf > ti$ : le corps s'est échauffé, il a reçu de l'énergie et $Q$ est positive.
Si $tf < ti$ : le corps s'est refroidi, il a donné de l'énergie et $Q$ est négative.

Capacité calorifique massique $C$ :
Elle intervient dans le calcul de la quantité de chaleur $Q$ perdue ou gagnée.
$C$ d'un corps est la quantité de chaleur qu'il faut fournir (ou prendre) à l'unité de masse de ce corps pour que sa température s'élève (ou s'abaisse) de 1° K

Pour céder $Q$, un corps dont $C$ est petit doit beaucoup se refroidir, si $C$ est élevé il se refroidit peu.

Expérience de Joule
Joule a montré que l’élévation de température d’un liquide peut être provoquée par un apport d'énergie mécanique (ex : Faire tourner une cuillère dans un verre d’eau)

Joule a démontré que l’unité de Q doit s’exprimer en Joules comme celle du travail mécanique W

Chaleur Latente (J/Kg) :
Elle traduit l’inertie du corps (l’opposition) du corps à changer de phase. C’est la chaleur que doit perdre ou gagner le corps pour que le changement de phase s’effectue (ex : vaporisation), et non pas pour augmenter sa température.

Pouvoir calorifique (Chaleur massique de combustion)
Le pouvoir calorifique est la quantité d’énergie fournie par la combustion d’un corps (c’est la conversion d’énergie chimique en chaleur).
Ex : L’essence apporte une chaleur qui est dégagée lors de sa combustion $Qc = M_{essence} \times L_{combustion}$


Travail des forces de pression

Les gaz sont des systèmes dont le volume varie beaucoup en fonction des échanges de chaleur. 

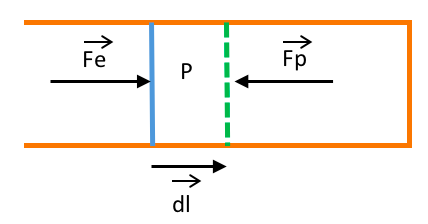
$Fp$ : Force de pression 
$P$ : Pression du gaz 
$dl$ : Déplacement dû à $Fe$
$Fe$ : Force extérieure
$S$ : Section du piston

Un cylindre renferme un gaz à la pression $P$.
Le gaz exerce alors une force pressante $Fp = P.S$
La variation du travail de $Fp$ du au déplacement $dl$ vaut : $d W = - P .d V$  $\boxed{d V : \text{variation du volume de gaz}}$
Compression : $d V < 0$ (le volume diminue) => $d W > 0$ le gaz reçoit du travail.
Détente : $d V > 0$ (le volume augmente) => $d W < 0$ le gaz fournit du travail au milieu extérieur.

QUATRE TRANSFORMATIONS DE BASE
Ces 4 transformations simples permettent de modéliser des transformations plus complexes et donnent une expression simple de W, Q ou W+Q. Les 3 premières transformations conservent une variable d’état constante.
• Isobare : Se fait à pression constante => $W = -P \times \Delta V$
• Isochore : Se fait à volume constant => $W=0$
• Isotherme : Se fait à T° constante => $W+Q = 0$
• Adiabatique : aucune chaleur n'est échangée avec l'extérieur : la transformation est très rapide et/ou calorifugée => $Q =0$ (la chaleur provoquée par la transformation n’a pas le temps de s’évacuer)

1ER PRINCIPE DE LA THERMODYNAMIQUE
Le 1er principe de la thermodynamique, basé sur la conservation d’énergie, permet de d’établir le signe et la valeur de ces variations.

Énergie interne :
Au cours d’une transformation, la variation d’énergie interne ΔU du système, est égale à l’énergie totale échangée avec l’extérieur :

$\Delta U = W + Q$      ($W$ et $Q$ sont $≤ 0$ s'ils sont perdus par le système)

Remarques : 

• L’énergie s’échange avec le milieu extérieur soit par échange de chaleur $(Q)$, soit par un travail fourni ou reçu : $W$
• Pour une transfo adiabatique $(Q = 0)$, on aura toujours $\Delta U = W$

CYCLE de transformation :

Deux transformations minimum sont nécessaires pour obtenir un cycle.

Un système effectue un cycle si son état final est équivalent à l'état initial (les grandeurs $P, V, T$ reviennent à leurs valeurs initiales).

$W_{cycle} = W_{A1B} + W_{B2A}$ (correspond à la surface hachurée donc surface engendrée par le cycle au signe près)

Un cycle est :

• moteur lorsque $W_{cycle} < 0$ car il fournit de l’énergie (parcours sens horaire)
• résistant lorsque $W_{cycle} > 0$

Remarque 1 : Cycle ⇒ pas de variation d'énergie interne 

⇒ $\Delta Ucycle = W + Q = 0 => W = -Q$ 

Le travail échangé est opposé à la quantité de chaleur échangée par le système.

Remarque 2 : Si la transformation est réversible (« retour » est identique à « l’aller ») : $W=0$

2e PRINCIPE DE LA THERMODYNAMIQUE
Il faut au moins deux sources de chaleur pour réaliser un moteur thermique.
Lors d'une transformation cyclique réversible et isotherme réalisée avec 2 sources de chaleur ($T_2 = Cte$ et $T_1 = Cte$), une quantité reste constante et elle est intégralement transférée de la source chaude vers la source froide.
On appelle cela la variation d’entropie. $\Delta S= (\frac{\Delta Q}{T})_{Rev}$
Illustration : Transfert thermique $\Delta Q$ entre deux corps (non isolés par rapport à l’extérieur)
Soit un système constitué de deux corps $C_1$ et $C_2$ respectivement à $T_1$ et $T_2$.
Le corps $C_1$ reçoit : $\Delta Q_1 = (\Delta Q_1)_{extérieur} + (\Delta Q_1)_{corps2}$          Pour $C_1$ : $\displaystyle \Delta S_1= \Delta_{ext}.S_1 =\frac{\Delta Q_1}{T_1}$ 
Le corps $C_2$ reçoit : $\displaystyle \Delta Q_2 = (\Delta Q_2)_{extérieur} + (\Delta Q_2)_{corps1}$          Pour $C_2$ : $\displaystyle \Delta S_2 = \Delta_{ext}.S_2 = \frac{\Delta Q_2}{T_2}$. 
D’où $\Delta S = \Delta S_1 + \Delta S_2$ et par identification $\Delta S = \Delta_{ext}S + \Delta_{corps}S$
$\boxed{\Delta_{ext} : \text{variation d'entropie / extérieur}}$

$\boxed{\Delta_{corps} : \text{variation d'entropie / corps}}$

Application au moteur thermique
C’est un cycle ditherme quelconque (réalisé en 3 étapes) utilisant 2 sources de températures extrêmes $T_1 < T_2$  

Le 2e principe => pour le cycle $\displaystyle \frac{Q_1}{T_1} + \frac{Q_2}{T_2} ≤ 0$ 
Remarque 1 : Un moteur thermique absorbe son énergie (chaleur) de la source chaude et en rejette une partie vers la source froide
Remarque 2 : Le travail restitué ne sera jamais être égal à la somme de chaleurs absorbées (sinon $\eta = 100%$)
Conclusion: Un moteur thermique rejettera toujours de la chaleur, il s'échauffera donc toujours.
Pour une transfo réversible $\eta_{max}=(1-\frac{T_1}{T_2}) \times 100$   
Remarque : $\eta_{max}$ dépend uniquement des températures des sources, elles doivent être pour $T_1$ la plus froide possible, pour $T_2$ la plus chaude possible.